
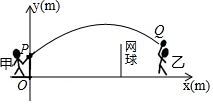
 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x-4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.
甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x-4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.分析 (1)①将点P(0,1)代入y=-$\frac{1}{24}$(x-4)2+h即可求得h;②求出x=5时,y的值,与1.55比较即可得出判断;
(2)将(0,1)、(7,$\frac{12}{5}$)代入y=a(x-4)2+h代入即可求得a、h.
解答 解:(1)①当a=-$\frac{1}{24}$时,y=-$\frac{1}{24}$(x-4)2+h,
将点P(0,1)代入,得:-$\frac{1}{24}$×16+h=1,
解得:h=$\frac{5}{3}$;
②把x=5代入y=-$\frac{1}{24}$(x-4)2+$\frac{5}{3}$,得:y=-$\frac{1}{24}$×(5-4)2+$\frac{5}{3}$=1.625,
∵1.625>1.55,
∴此球能过网;
(2)把(0,1)、(7,$\frac{12}{5}$)代入y=a(x-4)2+h,得:
$\left\{\begin{array}{l}{16a+h=1}\\{9a+h=\frac{12}{5}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{5}}\\{h=\frac{21}{5}}\end{array}\right.$,
∴a=-$\frac{1}{5}$.
点评 本题主要考查二次函数的应用,熟练掌握待定系数法求函数解析式是解题的关键.


科目:初中数学 来源: 题型:解答题
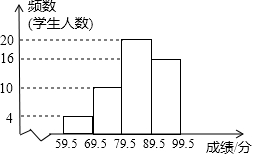 为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数.从中抽取部分同学的成绩进行统计,并绘制成如图统计图.
为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数.从中抽取部分同学的成绩进行统计,并绘制成如图统计图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2017年南宁市教育局组织全市中小学时候参加安全知识网络竞赛,在安全知识竞赛结束后,赛后发现所有参赛学生会的成绩都高于50分.为了了解本次大赛的成绩分布情况,某校随机抽取了其中200名学生的成绩(成绩x取整数,总分为100分)作为样本进行统计分析,得到如下不完整的统计图表,请根据图标中的信息解答下列各题:
2017年南宁市教育局组织全市中小学时候参加安全知识网络竞赛,在安全知识竞赛结束后,赛后发现所有参赛学生会的成绩都高于50分.为了了解本次大赛的成绩分布情况,某校随机抽取了其中200名学生的成绩(成绩x取整数,总分为100分)作为样本进行统计分析,得到如下不完整的统计图表,请根据图标中的信息解答下列各题:| 成绩(分) | 频数 | 频数 |
| 50<x≤60 | 10 | b |
| 60<x≤70 | 20 | 0.10 |
| 70<x≤80 | 30 | 0.15 |
| 80<x≤90 | a | 0.30 |
| 90<x≤100 | 80 | 0.40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
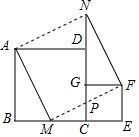 如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b-$\frac{{b}^{2}}{a}$;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )
如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b-$\frac{{b}^{2}}{a}$;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com