
【题目】如图,正方形ABCD中,E、F是对角线AC上两点,连接BE、BF、DE、DF,则添加下列条件①∠ABE=∠CBF;②AE=CF;③AB=AF;④BE=BF.可以判定四边形BEDF是菱形的条件有( )
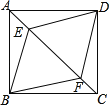
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据正方形的四条边都相等,对角线互相垂直平分且每一条对角线平分一组对角的性质,再加上各选项的条件,对各选项分析判断后即可得出正确选项的个数
解:如图,连接BD,交AC于点O,
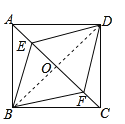
在正方形ABCD中,AB=BC,∠BAC=∠ACB,AC⊥BD,AO=CO,BO=DO,
①在△ABE与△BCF中,
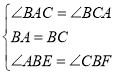 ,
,
∴△ABE≌△BCF(ASA),
∴BE=BF,
∵AC⊥BD,
∴OE=OF,
所以四边形BEDF是菱形,故①选项正确;
②在正方形ABCD中,AC=BD,
∴OA=OB=OC=OD,
∵AE=CF,
∴OE=OF,又EF⊥BD,BO=OD,
∴四边形BEDF是菱形,故②选项正确;
③AB=AF,不能推出四边形BEDF其它边的关系,故不能判定是菱形,本选项错误;
④BE=BF,同①的后半部分证明,故④选项正确.
所以①②④共3个可以判定四边形BEDF是菱形.
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】全善学校为了提高学生综合能力,培养学生兴趣,决定开设以下精品校本课程:A. 创新与实践,B. 数学之美,C.英美文学鉴赏,D. 小小外交家,为了解学生最喜欢哪一项校本课程,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
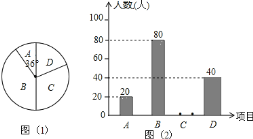
(1)这次被调查的学生共有______人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的小小外交家的课堂学习中,有三男一女四名同学表现优秀,现决定从这四名同学中任选两名参加全国英语口语大赛,求恰好选到一男一女两位同学的概率(用树状图或列表法解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地始往乙地,一列慢车从乙地始往甲地,慢车的速度是快车速度的![]() ,两车同时出 发.设慢车行驶的时间为
,两车同时出 发.设慢车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() ,图中的折线表示
,图中的折线表示![]() 与
与![]() 之间的函数关系.根据图象解决以下问题:
之间的函数关系.根据图象解决以下问题:
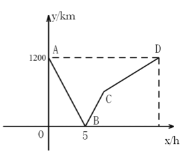
(1)甲、乙两地之间的距离为_______![]() ;点
;点![]() 的坐标为__________;
的坐标为__________;
(2)求线段![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)若第二列快车从乙地出发驶往甲地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车追上慢车.求第二列快车比第一列快车晚出发多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
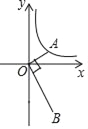
【题目】如图,已知点A是反比例y=![]() (x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为_____.
(x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 B、D、E 在一条直线上,BE 与 AC 相交于点 F,![]() ,连接 EC.
,连接 EC.
(1)求证:△ABD∽△ACE;
(2)若∠BAD=21°,求∠EBC 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
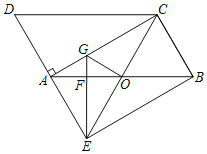
【题目】如图,在平行四边形ABCD中,![]() ,延长DA于点E,使得
,延长DA于点E,使得![]() ,连接BE.
,连接BE.
![]() 求证:四边形AEBC是矩形;
求证:四边形AEBC是矩形;
![]() 过点E作AB的垂线分别交AB,AC于点F,G,连接CE交AB于点O,连接OG,若
过点E作AB的垂线分别交AB,AC于点F,G,连接CE交AB于点O,连接OG,若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
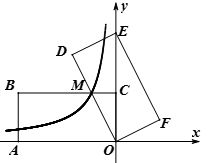
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在轴的负半轴、轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y=![]() (x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=
(x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=![]() ,,则BN的长为______________.
,,则BN的长为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数,如![]() 就是一个“中高数”.若十位上数字为
就是一个“中高数”.若十位上数字为![]() ,则从
,则从![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中任选两个不同的数,与
中任选两个不同的数,与![]() 组成“中高数”的概率是________.
组成“中高数”的概率是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com