
【题目】如图,在正方形![]() 中,点E在边
中,点E在边![]() 上,将点E绕点D逆时针旋转得到点F,若点F恰好落在边
上,将点E绕点D逆时针旋转得到点F,若点F恰好落在边![]() 的延长线上,连接
的延长线上,连接![]() ,
,![]() ,
,![]() .
.
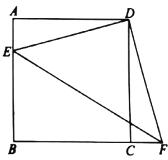
(1)判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)若![]() ,则
,则![]() 的面积为________.
的面积为________.
【答案】(1)![]() 是等腰直角三角形,理由见详解;(2)8.
是等腰直角三角形,理由见详解;(2)8.
【解析】
(1)根据条件,易证:RtDAERt DCF,即:∠ADE=∠CDF,进而可得![]() 是等腰直角三角形;
是等腰直角三角形;
(2)根据等腰直角三角形三边的比例关系,可得:DE=DF=![]() =4,进而可求面积.
=4,进而可求面积.
(1)∵在正方形![]() 中,点E在边
中,点E在边![]() 上,将点E绕点D逆时针旋转得到点F,
上,将点E绕点D逆时针旋转得到点F,
∴DE=DF,DA=DC,∠DAE=∠DCF=90°,
在RtDAE和Rt DCF中,
∵![]()
∴RtDAERt DCF(HL),
∴∠ADE=∠CDF,
∴∠EDF=∠EDC+∠CDF=∠EDC+∠ADE=∠ADC=90°,
∴![]() 是等腰直角三角形;
是等腰直角三角形;
(2)∵![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,
∴DE=DF=![]() =4,
=4,
∴![]() 的面积=4×4÷2=8.
的面积=4×4÷2=8.
故答案是:8.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】2019年5月,以“寻根国学,传承文明”为主题的兰州市第三届“国学少年强一国学知识挑战赛”总决赛拉开帷幕,小明晋级了总决赛.比赛过程分两个环节,参赛选手须在每个环节中各选择一道题目.
第一环节:写字注音、成语故事、国学常识、成语接龙(分别用![]() 表示);
表示);
第二环节:成语听写、诗词对句、经典通读(分别用![]() 表示)
表示)
(1)请用树状图或列表的方法表示小明参加总决赛抽取题目的所有可能结果
(2)求小明参加总决赛抽取题目都是成语题目(成语故事、成语接龙、成语听写)的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,抛物线顶点为
,抛物线顶点为![]() ,下列四个结论:①无论
,下列四个结论:①无论![]() 取何值,
取何值,![]() 恒成立;②当
恒成立;②当![]() 时,
时,![]() 是等腰直角三角形;③若
是等腰直角三角形;③若![]() 则
则![]() ;④抛物线上有两点
;④抛物线上有两点![]() 和
和![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() .其中正确的结论是( )
.其中正确的结论是( )
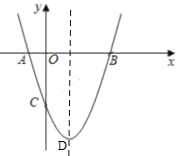
A.①②④B.②③④C.①②D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个工程队共同参与一项筑路工程,甲队单独施工3个月,这时增加了乙队,两队又共同工作了2个月,总工程全部完成,已知甲队单独完成全部工程比乙队单独完成全部工程多用2个月,设甲队单独完成全部工程需![]() 个月,则根据题意可列方程中错误的是( )
个月,则根据题意可列方程中错误的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 为半径作优弧
为半径作优弧![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .点
.点![]() 在优弧
在优弧![]() 上从点
上从点![]() 开始移动,到达点
开始移动,到达点![]() 时停止,连接
时停止,连接![]() .
.
(1)当![]() 时,判断
时,判断![]() 与优弧
与优弧![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)当![]() 时,求点
时,求点![]() 在优弧
在优弧![]() 上移动的路线长及线段
上移动的路线长及线段![]() 的长.
的长.
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
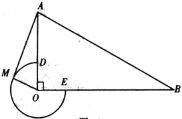
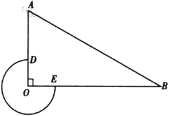
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() ﹔
﹔![]() 与
与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 的顶点为
的顶点为![]() ,直线
,直线![]() .
.
(1)当![]() 时,画出直线
时,画出直线![]() 和抛物线
和抛物线![]() ,并直接写出直线
,并直接写出直线![]() 被抛物线
被抛物线![]() 截得的线段长.
截得的线段长.
(2)随着![]() 取值的变化,判断点
取值的变化,判断点![]() 是否都在直线
是否都在直线![]() 上并说明理由.
上并说明理由.
(3)若直线![]() 被抛物线
被抛物线![]() 截得的线段长不小于3,结合函数的图像,直接写出
截得的线段长不小于3,结合函数的图像,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技发展,社会进步,中国已进入特色社会主义新时代,为实现“两个一百年”奋斗目标和中华民族伟大复兴的中国梦,需要人人奋斗,青少年时期是良好品格形成和知识积累的黄金时期,为此,大数据平台针对部分中学生品格表现和学习状况进行调查统计绘制如下统计图表,请根据图中提供的信息解决下列问题,类别:![]() 品格健全,成绩优异;
品格健全,成绩优异;![]() 尊敬师长,积极进取;
尊敬师长,积极进取;![]() 自控力差,被动学习;
自控力差,被动学习;![]() 沉迷奢玩,消极自卑.
沉迷奢玩,消极自卑.
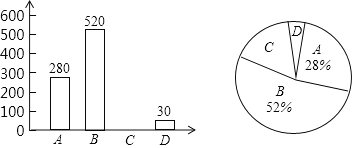
(1)本次调查被抽取的样本容量为 ;
(2)“自控力差,被动学习”的同学有 人,并补全条形统计图;
(3)样本中![]() 类所在扇形的圆心角为 度;
类所在扇形的圆心角为 度;
(4)东至县城内某中学有在校学生3330人,请估算该校![]() 类学生人数.
类学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
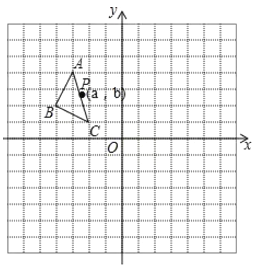
【题目】如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上.
(1)将△ABC向下平移5个单位再向右平移1个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)P(a,b)是△ABC的边AC上一点,请直接写出经过两次变换后在△A2B2C2中对应的点P2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c的图象与x轴交于A(﹣4,0)和点B两点,与y轴交于点C,抛物线的对称轴是x=﹣1与x轴交于点D.
(1)求拋物线的函数表达式;
(2)若点P(m,n)为抛物线上一点,且﹣4<m<﹣1,过点P作PE∥x轴,交抛物线的对称轴x=﹣1于点E,作PF⊥x轴于点F,得到矩形PEDF,求矩形PEDF周长的最大值;
(3)点Q为抛物线对称轴x=﹣1上一点,是否存在点Q,使以点Q,B,C为顶点的三角形是直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com