
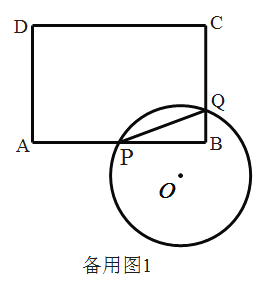
【题目】如图,已知矩形![]() 的边
的边![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的动点.
边上的动点.

(1)连接![]() 、
、![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() .
.
①若点![]() 恰好是
恰好是![]() 的中点,则
的中点,则![]() 与
与![]() 的数量关系是______;
的数量关系是______;
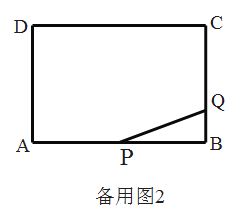
②若![]() ,求
,求![]() 的长;
的长;
(2)已知![]() ,
,![]() ,
,![]() 是以
是以![]() 为弦的圆.
为弦的圆.
①若圆心![]() 恰好在
恰好在![]() 边的延长线上,求
边的延长线上,求![]() 的半径:
的半径:
②若![]() 与矩形
与矩形![]() 的一边相切,求
的一边相切,求![]() 的半径.
的半径.
【答案】(1)①![]() ;②1.5;(2)①5;②
;②1.5;(2)①5;②![]() 、
、![]() ,
,![]() 、5.
、5.
【解析】
(1)①根据直径所对的圆周角是直角判断△APQ为等腰三角形,结合等腰三角形的两底角相等和圆周角定理证明;②证明△PBQ∽△QBA,由对应边成比例求解;
(2)①画出图形,由勾股定理列方程求解;②分![]() 与矩形
与矩形![]() 的四边分别相切,画出图形,利用切线性质,由勾股定理列方程求解.
的四边分别相切,画出图形,利用切线性质,由勾股定理列方程求解.
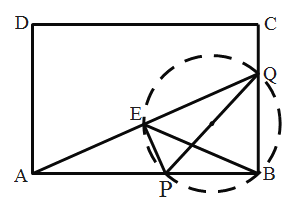
解:(1)①如图,PQ是直径,E在圆上,
∴∠PEQ=90°,
∴PE⊥AQ,
∵AE=EQ,
∴PA=PQ,
∴∠PAQ=∠PQA,
∴∠QPB=∠PAQ+∠PQA=2∠AQP,
∵∠QPB=2∠AQP.
 \
\
②解:如图,∵BE=BQ=3,
∴∠BEQ=∠BQE,
∵∠BEQ=∠BPQ,
∵∠PBQ=∠QBA,
∴△PBQ∽△QBA,
∴![]() ,
,
∴![]() ,
,
∴BP=1.5;

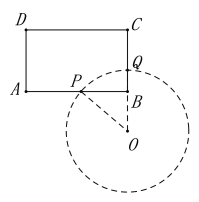
(2)①如图, BP=3,BQ=1,设半径OP=r,
在Rt△OPB中,根据勾股定理得,PB2+OB2=OP2
∴32+(r-1)2=r2,
∴r=5,
∴![]() 的半径是5.
的半径是5.
②如图,![]() 与矩形
与矩形![]() 的一边相切有4种情况,
的一边相切有4种情况,
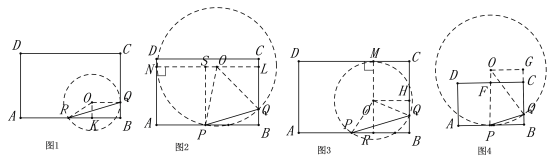
如图1,当![]() 与矩形ABCD边BC相切于点Q,过O作OK⊥AB于K,则四边形OKBQ为矩形,
与矩形ABCD边BC相切于点Q,过O作OK⊥AB于K,则四边形OKBQ为矩形,
设OP=OQ=r,则PK=3x,
由勾股定理得,r2=12+(3-r)2,
解得,r=![]() ,
,
∴![]() 半径为
半径为![]() .
.
如图2,当![]() 与矩形ABCD边AD相切于点N,延长NO交BC于L,则OL⊥BC,过P作PS⊥NL于S,
与矩形ABCD边AD相切于点N,延长NO交BC于L,则OL⊥BC,过P作PS⊥NL于S,
设OS=x,则ON=OP=OQ=3+x,设PS=BL=y,
由勾股定理得,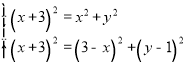 ,
,
解得![]() (舍去),
(舍去),![]() ,
,
∴ON=![]() ,
,
∴![]() 半径为
半径为![]() .
.
如图3,当![]() 与矩形ABCD边CD相切于点M,延长MO交AB于R,则OR⊥AB,过O作OH⊥BC于H,
与矩形ABCD边CD相切于点M,延长MO交AB于R,则OR⊥AB,过O作OH⊥BC于H,
设OH=BR=x,设HQ=y, 则OM=OP=OQ=4-1-y=3-y,
由勾股定理得,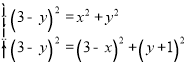 ,
,
解得![]() (舍去),
(舍去),![]() ,
,
∴OM=![]() ,
,
∴![]() 半径为
半径为![]() .
.
如图4,当![]() 与矩形ABCD边AB相切于点P,过O作OG⊥BC于G,则四边形AFCG为矩形,
与矩形ABCD边AB相切于点P,过O作OG⊥BC于G,则四边形AFCG为矩形,
设OF=CG=x,,则OP=OQ=x+4,
由勾股定理得(x+4)2=32+(x+3)2,
解得,x=1,
∴OP=5,
∴![]() 半径为5.
半径为5.
综上所述,若![]() 与矩形
与矩形![]() 的一边相切,为
的一边相切,为![]() 的半径
的半径![]() ,
,![]() ,
,![]() ,5.
,5.


科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC.点D是线段AC上一点,连接BD.过点C作CE⊥BD于点E.点F是AB垂直平分线上一点,连接BF、EF.
(1)若AD=4![]() ,tan∠BCE=
,tan∠BCE=![]() ,求AB的长;
,求AB的长;
(2)当点F在AC边上时,求证:∠FEC=45°.

查看答案和解析>>
科目:初中数学 来源: 题型:
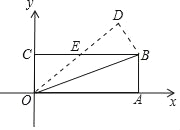
【题目】如图,平面直角坐标中,把矩形OABC沿对角线OB所在的直线折叠,点A落在点D处,OD与BC交于点E.OA、OC的长是关于x的一元二次方程x2﹣9x+18=0的两个根(OA>OC).
(1)求A、C的坐标.
(2)直接写出点E的坐标,并求出过点A、E的直线函数关系式.
(3)点F是x轴上一点,在坐标平面内是否存在点P,使以点O、B、P、F为顶点的四边形为菱形?若存在请直接写出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 、
、![]() 为常数)的图像经过点
为常数)的图像经过点![]() 和点
和点![]() .
.
(1)求![]() 、
、![]() 的值;
的值;
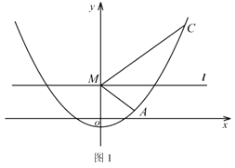
(2)如图1,点![]() 在抛物线上,点
在抛物线上,点![]() 是
是![]() 轴上的一个动点,过点
轴上的一个动点,过点![]() 平行于
平行于![]() 轴的直线
轴的直线![]() 平分
平分![]() ,求点
,求点![]() 的坐标;
的坐标;
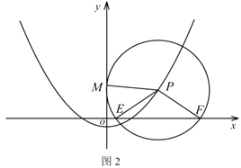
(3)如图2,在(2)的条件下,点![]() 是抛物线上的一动点,以
是抛物线上的一动点,以![]() 为圆心、
为圆心、![]() 为半径的圆与
为半径的圆与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,请直接写出点
,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
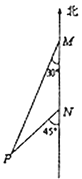
【题目】2019年12月17日,我国第一艘国产航母“山东舰”在海南三亚交付海军.如图,“山东舰”在一次试水测试中,航行至![]() 处,观测指挥塔
处,观测指挥塔![]() 位于南偏西
位于南偏西![]() 方向,在沿正南方向以30海里/小时的速度匀速航行2小时后,到达
方向,在沿正南方向以30海里/小时的速度匀速航行2小时后,到达![]() 处,再观测指挥塔
处,再观测指挥塔![]() 位于南偏西
位于南偏西![]() 方向,若继续向南航行.求“山东舰”与指挥塔之间的最近距离为多少海里?(结果保留根号)
方向,若继续向南航行.求“山东舰”与指挥塔之间的最近距离为多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
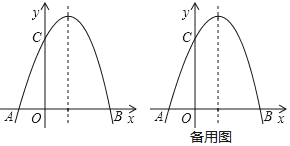
【题目】已知,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P,使PA+PC的值最小?如果存在,请求出点P的坐标,如果不存在,请说明理由;(3)设点M在抛物线的对称轴上,当△MAC是直角三角形时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
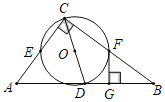
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,连接CD,点O是CD的中点,到点O的距离等于OC的所有点组成图形M,图形M分别交AC,BC于点E,F两点,过点F作FG⊥AB于点G.
(1)试判断FG与图形M的位置关系,并说明理由;
(2)若AC=3,∠B=30°,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解朝阳社区![]() 岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
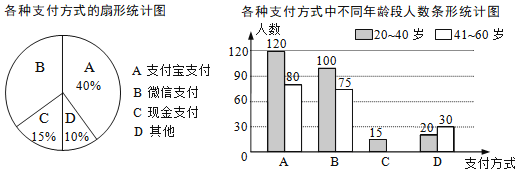
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中![]() 岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
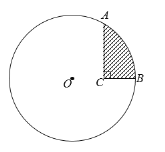
【题目】如图,⊙O的半径为![]() ,A、B为⊙O上两点,C为⊙O内一点,AC⊥BC,AC=
,A、B为⊙O上两点,C为⊙O内一点,AC⊥BC,AC=![]() ,BC=
,BC=![]() .
.
(1)判断点O、C、B的位置关系;
(2)求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com