
【题目】已知在△ABC中,∠ABC=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
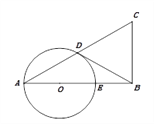
(1)求证: ![]() ;
;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
【答案】(1)证明见解析;(2)4.
【解析】试题分析:(1)本题利用两角法判定三角形相似,利用相似三角形的性质得出比例式即可;(2)利用切线的性质和特殊角的三角函数值判断出∠OBD=30°,进而得出∠BAC=30°,利用30°所对的直角边是斜边的一半即可得出.
试题解析:
(1)证明:连接DE,
∵AE是直径,∴∠ADE=90°.
∴∠ADE=∠ABC.
又∠A=∠A,∴△ADE∽△ABC. (3分)
∴![]() . (4分)
. (4分)
(2)解:连接OD,
∵BD是⊙O的切线,
∴OD⊥BD
∴∠ODB=90°. (5分)
∵在Rt△OBD中,E是OB的中点,
∴DE= ![]() =BE=OE=OD, (6分)
=BE=OE=OD, (6分)
∴sin∠OBD=![]() .
.
∴∠OBD=30° (7分)
同理∠BAC=30°. (8分)
在Rt△ABC中,AC=2BC=2×2=4.(9分)


科目:初中数学 来源: 题型:
【题目】某校规定学生的学期数学成绩满分为100分,其中平时学习成绩占30%,期末卷面成绩占70%,小明的两项成绩(百分制)依次是80分,90分,则小明这学期的数学成绩是( )
A. 83分B. 86分C. 87分D. 92.4分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工人若每小时生产38个零件,在规定时间内还有15个不能完成,若每小时生产42个零件,则可以超额完成5个,问:规定时间是多少?设规定时间为x小时,则可列方程为( )
A. 38x﹣15=42x+5 B. 38x+15=42x﹣5 C. 42x+38x=15+5 D. 42x﹣38x=15﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( ) 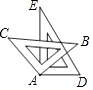
A.∠BAD≠∠EAC
B.∠DAC﹣∠BAE=45°
C.∠BAE+∠DAC=180°
D.∠DAC>∠BAE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某下岗职工购进一批货物,到集贸市场零售,已知卖出去的货物数量x与售价y的关系如下表:
数量x(千克) | 1 | 2 | 3 | 4 | 5 |
售价y(元) | 3+0.1 | 6+0.2 | 9+0.3 | 12+0.4 | 15+0.5 |
写出用x表示y的公式是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个判断:①当x>0时,y>0;②若a=-1,则b=4;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1< x2,且x1+x2>2,则y1> y2;④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为6![]() .其中正确判断的序号是( )
.其中正确判断的序号是( )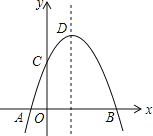
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
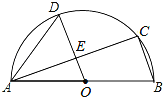
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=72°,求∠CAD的度数;
(2)若AB=13,AC=12,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com