Question

15．如图，在矩形ABCD中，AD=acm，AB=bcm（a＞b＞4），半径为2cm的⊙O在矩形内且与AB、AD均相切，现有动点P从A点出发，在矩形边上沿着A→B→C→D的方向匀速移动，当点P到达D点时停止移动．⊙O在矩形内部沿AD向右匀速平移，移动到与CD相切时立即沿原路按原速返回，当⊙O回到出发时的位置（即再次与AB相切）时停止移动，已知点P与⊙O同时开始移动，同时停止移动（即同时到达各自的终止位置）．
（1）如图①，点P从A→B→C→D，全程共移动了a+2bcm（用含a、b的代数式表示）；
（2）如图①，已知点P从A点出发，移动2s到达B点，继续移动3s，到达BC的中点，若点P与⊙O的移动速度相等，求在这5s时间内圆心O移动的距离；
（3）如图②，已知a=20，b=10，是否存在如下情形：当⊙O到达⊙O₁的位置时（此时圆心O₁在矩形对角线BD上），DP与⊙O₁恰好相切？请说明理由．

Answer 1

分析 （1）根据有理数的加法，可得答案；
（2）根据圆O移动的距离与P点移动的距离相等，P点移动的速度相等，可得方程组，根据解方程组，可得a、b的值，根据速度与时间的关系，可得答案；
（3）根据相同时间内速度的比等于路程的比，可得$\frac{{v}_{1}}{{v}_{2}}$的值，根据相似三角形的性质，可得∠ADB=∠BDP，根据等腰三角形的判定，可得BP与DP的关系，根据勾股定理，可得DP的长，根据有理数的加法，可得P点移动的距离；根据相似三角形的性质，可得EO₁的长，分类讨论：当⊙O首次到达⊙O₁的位置时，当⊙O在返回途中到达⊙O₁位置时，根据$\frac{{v}_{1}}{{v}_{2}}$的值，可得答案．

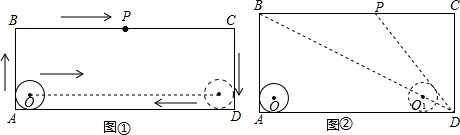
解答 解：（1）如图①，点P从A→B→C→D，全程共移动了 a+2bcm（用含a、b的代数式表示）；
（2）∵圆心O移动的距离为2（a-4）cm，
由题意，得
a+2b=2（a-4）①，
∵点P移动2秒到达B，即点P2s移动了bcm，点P继续移动3s到达BC的中点，
即点P3秒移动了$\frac{1}{2}$acm．
∴$\frac{b}{2}$=$\frac{\frac{1}{2}a}{3}$   ②
由①②解得$\left\{\begin{array}{l}{a=24}\\{b=8}\end{array}\right.$，
∵点P移动的速度为与⊙O移动速度相同，
∴⊙O移动的速度为$\frac{b}{2}$=$\frac{8}{2}$=4cm（cm/s）．
这5秒时间内⊙O移动的距离为5×4=20（cm）；
（3）存在这种情况，
设点P移动速度为v₁cm/s，⊙O₂移动的速度为v₂cm/s，
由题意，得
$\frac{{v}_{1}}{{v}_{2}}$=$\frac{a+2b}{2（a-4）}$=$\frac{20+2×10}{2（20-4）}$=$\frac{5}{4}$，
如图：
设直线OO₁与AB交于E点，与CD交于F点，⊙O₁与AD相切于G点，
若PD与⊙O₁相切，切点为H，则O₁G=O₁H．
易得△DO₁G≌△DO₁H，
∴∠ADB=∠BDP．
∵BC∥AD，
∴∠ADB=∠CBD
∴∠BDP=∠CBD，
∴BP=DP．
设BP=xcm，则DP=xcm，PC=（20-x）cm，
在Rt△PCD中，由勾股定理，得
PC²+CD²=PD²，即（20-x）²+10²=x²，
解得x=$\frac{25}{2}$
此时点P移动的距离为10+$\frac{25}{2}$=$\frac{45}{2}$（cm），
∵EF∥AD，
∴△BEO₁∽△BAD，
∴$\frac{E{O}_{1}}{AD}$=$\frac{BE}{BA}$，即$\frac{E{O}_{1}}{20}$=$\frac{8}{10}$，
EO₁=16cm，OO₁=14cm．
①当⊙O首次到达⊙O₁的位置时，⊙O移动的距离为14cm，
此时点P与⊙O移动的速度比为$\frac{\frac{45}{2}}{14}$=$\frac{45}{28}$，
∵$\frac{45}{28}$≠$\frac{5}{4}$，
∴此时PD与⊙O₁不能相切；
②当⊙O在返回途中到达⊙O₁位置时，⊙O移动的距离为2（20-4）-14=18cm，
∴此时点P与⊙O移动的速度比为$\frac{\frac{45}{2}}{18}$=$\frac{45}{36}$=$\frac{5}{4}$，
此时PD与⊙O₁恰好相切．

点评 本题考查了圆的综合题，（1）利用了有理数的加法，（2）利用了P与⊙O的路程相等，速度相等得出方程组是解题关键，再利用路程与时间的关系，得出速度，最后利用速度乘以时间得出结果；（3）利用了相等时间内速度的比等于路程的比，相似三角形的性质，等腰三角形的判定，勾股定理，利用相等时间内速度的比等于路程的比是解题关键．