
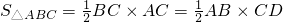 ,可得到CD=2.4
,可得到CD=2.4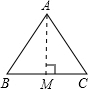 解:(1)∵∠C=90°,BC=5,AC=12,
解:(1)∵∠C=90°,BC=5,AC=12, BC×AC=
BC×AC= AB×CD,
AB×CD, ;
; ,
, …2′,
…2′, BC×
BC× =
= AB×DE+
AB×DE+ AC×DF,
AC×DF, BC=AB•DE+AC•DF
BC=AB•DE+AC•DF BC=AB•DE+AB•DF
BC=AB•DE+AB•DF BC=AB(DE+DF),
BC=AB(DE+DF), …3′.
…3′. BC×AC=
BC×AC= AB×CD,代入数据即可得出CD;
AB×CD,代入数据即可得出CD;

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:

| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江宁波地八年级第一次质量评估数学试卷(带解析) 题型:解答题
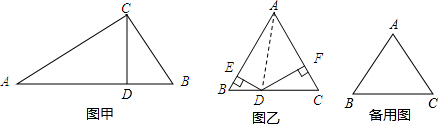
利用“等积”计算或说理是一种很巧妙的方法, 就是一个面积从两个不同的角度表示。如图甲,已知Rt△ABC中,∠C=90°,CD⊥AB于D,BC=3,AC=4,求CD的长。
解题思路:利用勾股定理易得AB=5利用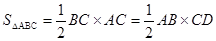 ,可得到CD=2.4
,可得到CD=2.4
请你利用上述方法解答下面问题:
(1) 如图甲,已知Rt△ABC中,∠C=90°,CD⊥AB于D,BC=5,AC=12,求CD的长。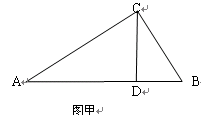
(2)如图乙,△ABC是边长为2的等边三角形,点D是BC边上的
任意一点,DE⊥AB于E点,DF⊥AC于F点,求DE+DF的值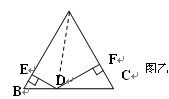
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江宁波地八年级第一次质量评估数学试卷(解析版) 题型:解答题
利用“等积”计算或说理是一种很巧妙的方法, 就是一个面积从两个不同的角度表示。如图甲,已知Rt△ABC中,∠C=90°,CD⊥AB于D,BC=3,AC=4,求CD的长。
解题思路:利用勾股定理易得AB=5利用
 ,可得到CD=2.4
,可得到CD=2.4
请你利用上述方法解答下面问题:
(1) 如图甲,已知Rt△ABC中,∠C=90°,CD⊥AB于D,BC=5,AC=12,求CD的长。
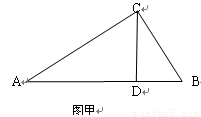
(2)如图乙,△ABC是边长为2的等边三角形,点D是BC边上的
任意一点,DE⊥AB于E点,DF⊥AC于F点,求DE+DF的值
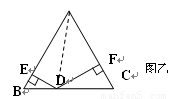
查看答案和解析>>
科目:初中数学 来源: 题型:
利用“等积”计算或说理是一种很巧妙的方法, 就是一个面积从两个不同的角度表示。如图甲,已知Rt△ABC中,∠C=90°,CD⊥AB于D,BC=3,AC=4,求CD的长。
解题思路:利用勾股定理易得AB=5利用
![]() ,可得到CD=2.4
,可得到CD=2.4
请你利用上述方法解答下面问题:
(1) 如图甲,已知Rt△ABC中,∠C=90°,CD⊥AB于D,BC=5,AC=12,求CD的长。
|

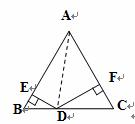
(2)如图乙,△ABC是边长为2的等边三角形,点D是BC边上的任意一点,DE⊥AB于E点,DF⊥AC于F点,求DE+DF的值
|
分析:①利用备用图计算等边三角形ABC高线的长度②连接AD,利用![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com