
【题目】如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
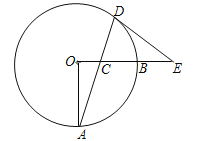
(1)求证:∠ECD=∠EDC;
(2)若tanA=![]() ,求DE长;
,求DE长;
(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.
【答案】(1)证明见解析;
(2)DE的长为15;
(3)弦AD在圆内扫过的面积为![]()
【解析】试题分析:(1)连结OD,已知DE是⊙O的切线,根据切线的性质可得∠EDC+∠ODA=90°,已知 OA⊥OB,可得∠ACO+∠A=90°,因OA=OD,根据等腰三角形的性质可得∠ODA=∠A,即可得∠EDC=∠ACO,因∠ECD=∠ACO,即可得∠ECD=∠EDC.(2)因为tanA=![]() ,即可得
,即可得![]() ,求得OC=2, 设DE=x,可得CE=x,所以OE=2+x,在Rt△ODE中,根据勾股定理可得OD2+DE2=OE2, 即可得82+x 2=(2+x)2,解得x=15,所以DE=CE=15. (3)过点D作AO的垂线,交AO的延长于F,当
,求得OC=2, 设DE=x,可得CE=x,所以OE=2+x,在Rt△ODE中,根据勾股定理可得OD2+DE2=OE2, 即可得82+x 2=(2+x)2,解得x=15,所以DE=CE=15. (3)过点D作AO的垂线,交AO的延长于F,当![]() 时,
时, ![]() ,DF=4,求得
,DF=4,求得![]() 的面积,当
的面积,当![]() 时,
时, ![]() ,DF=4
,DF=4![]() ,求得
,求得![]() ,即可求得弦AD在圆内扫过的面积.
,即可求得弦AD在圆内扫过的面积.
试题解析:
(1)证明:连结OD,
∵DE是⊙O的切线,∴∠EDC+∠ODA=900,
又∵OA⊥OB,∴∠ACO+∠A=900,
∵OA=OD,∴∠ODA=∠A,∴∠EDC=∠ACO,
又∵∠ECD=∠ACO,∴∠ECD=∠EDC.
(2)解:∵tanA=![]() ,∴
,∴![]() ,∴OC=2,
,∴OC=2,
设DE=x,∵∠ECD=∠EDC,∴CE=x,∴OE=2+x.
∴∠ODE=900,∴OD2+DE2=OE2,
∴82+x 2=(2+x)2,x=15,∴DE=CE=15.
(3)解:过点D作AO的垂线,交AO的延长于F,
当![]() 时,
时, ![]() ,DF=4,
,DF=4,
![]()
当![]() 时,
时, ![]() ,DF=4
,DF=4![]() ,
,
![]() ,
,
![]()
![]()
![]()


科目:初中数学 来源: 题型:
【题目】下列二次函数中,顶点坐标为(-5,0),且开口方向、形状与y=-x2的图象相同的是( )
A.y=(x-5)2B.y=x2-5C.y=-(x+5)2D.y=(x+5)2
查看答案和解析>>
科目:初中数学 来源: 题型:
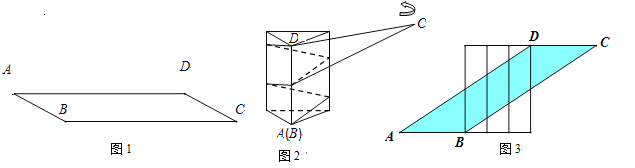
【题目】一张宽为6cm的平行四边形纸带ABCD如图1所示,AB=10cm,小明用这张纸带将底面周长为10cm直三棱柱纸盒的侧面进行包贴(要求包贴时没有重叠部分). 小明通过操作后发现此类包贴问题可将直三棱柱的侧面展开进行分析.
(1)若纸带在侧面缠绕三圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则纸带AD的长度为____ cm;
(2)若AD=100cm,纸带在侧面缠绕多圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则这个直三棱柱纸盒的高度是_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三淅高速2015年建成通车,三门峡到南阳全长291.6千米,将291.6千米用科学记数法表示为( )
A.2.916×106米
B.2.916×105米
C.29.16×105米
D.2.916×104米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人从少年宫出发,沿相同的路线分别以不同的速度匀速跑向体育馆,甲先跑一段路程 后,乙开始出发,当乙超出甲 150 米时,乙停在原地等候甲,两人相遇后乙又继续以原来的速度跑向体育馆.如图所示是甲、乙两人在跑步的全过程中经过的路程 y(米)与甲出发的时间 x(秒)之间关系的图象.
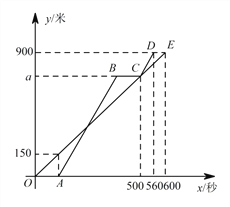
(1) 在跑步的全过程中,甲一共跑了 米,甲的速度为 米/秒.
(2) 求图中标注的 a 的值及乙跑步的速度.
(3) 乙在途中等候了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校5个小组参加植树活动,平均每组植树10株.已知第一,二,三,五组分别植树9株、12株、9株、8株,那么第四小组植树( )
A. 12株 B. 11株 C. 10株 D. 9株
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣5,3)、B(﹣2,﹣2)、C(﹣3,4). 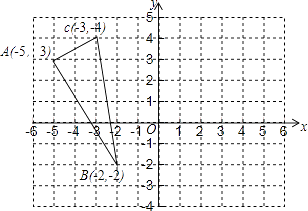
(1)作出△ABC关于y轴对称的△A1B1C1;
(2)写出点A关于x轴对称的点A2的坐标;
(3)△ABC的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com