
【题目】某服装店在服装销售中发现:进货价每件60元,销售价每件100元的某服装每天可售出20件,为了迎接新春佳节,服装店决定采取适当的促销措施,扩大销售量,增加盈利.经调查发现:如果每件服装降价1元,那么每天就可多售出2件.
(1)如果服装店想每天销售这种服装盈利1050元,同时又要使顾客得到更多的实惠,那么每件服装应降价多少元?
(2)每件服装降价多少元时,服装店每天可获得最大利润?最大利润是多少元?
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中(如图),已知二次函数
中(如图),已知二次函数![]() (其中a、b、c是常数,且a≠0)的图像经过点A(0,-3)、B(1,0)、C(3,0),联结AB、AC.
(其中a、b、c是常数,且a≠0)的图像经过点A(0,-3)、B(1,0)、C(3,0),联结AB、AC.
(1)求这个二次函数的解析式;
(2)点D是线段AC上的一点,联结BD,如果![]() ,求tan∠DBC的值;
,求tan∠DBC的值;
(3)如果点E在该二次函数图像的对称轴上,当AC平分∠BAE时,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知将抛物线![]() 沿
沿![]() 轴向上翻折与所得抛物线围成一个封闭区域(包括边界),在这个区域内有5个整点(点
轴向上翻折与所得抛物线围成一个封闭区域(包括边界),在这个区域内有5个整点(点![]() 满足横、纵坐标都为整数,则把点
满足横、纵坐标都为整数,则把点![]() 叫做“整点”).现将抛物线
叫做“整点”).现将抛物线![]() 沿
沿![]() 轴向下翻折,所得抛物线与原抛物线所围成的封闭区域内(包括边界)恰有11个整点,则
轴向下翻折,所得抛物线与原抛物线所围成的封闭区域内(包括边界)恰有11个整点,则![]() 的取值范围是( )
的取值范围是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一块锐角三角形余料,边BC=120 mm,高AD=80mm,要把它加工成矩形零件PQMN,使矩形PQMN的边QM在BC上,其余两个项点P,N分别在AB,AC上.
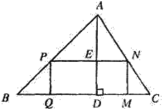
(1)当矩形的边PN=PQ时,求此时矩形零件PQMN的面积;
(2)求这个矩形零件PQMN面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,以AB为直径画弧分别交BC于点F,交对角线AC于点E,若AB=4,F为BC的中点,则图中阴影部分的面积为 ________;
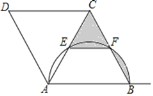
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区门口的栏杆从水平位置AB绕固定点O旋转到位置DC,已知栏杆AB的长为3.5米,OA的长为3米,点C到AB的距离为0.3米,支柱OE的高为0.6米,那么栏杆端点D离地面的距离为____________米

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,对称轴为直线x = -2的抛物线经过点C(0,2),与x轴交于A(-3,0)、B两点(点A在点B的左侧).
(1)求这条抛物线的表达式.
(2)连接BC,求∠BCO的余切值.
(3)如果过点C的直线,交x轴于点E,交抛物线于点P,且∠CEO =∠BCO,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一点O,使OB=OC,以点O为圆心,OB为半径作圆,过点C作CD∥AB交⊙O于点D,连接BD.
(1)猜想AC与⊙O的位置关系,并证明你的猜想;
(2)试判断四边形BOCD的形状,并证明你的判断;
(3)已知AC=6,求扇形OBC所围成的圆锥的底面圆的半径r.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com