
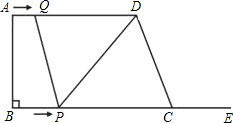
 如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).
如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).分析 (1)由题意已知,AD∥BC,要使四边形PQDC是平行四边形,则只需要让QD=PC即可,因为Q、P点的速度已知,AD、BC的长度已知,要求时间,用时间=路程÷速度,即可求出时间;
(2)要使以C、D、Q、P为顶点的梯形面积等于60cm2,可以分为两种情况:点P、Q分别沿AD、BC运动或点P返回时,再利用梯形面积公式,即(QD+PC)×AB÷2=60,因为Q、P点的速度已知,AD、AB、BC的长度已知,用t可分别表示QD、BC的长,即可求得时间t;
(3)使△PQD是等腰三角形,可分三种情况,即PQ=PD、PQ=QD、QD=PD;可利用等腰三角形及直角梯形的性质,分别用t表达等腰三角形的两腰长,再利用两腰相等即可求得时间t.
解答 解:(1)∵四边形PQDC是平行四边形,
∴DQ=CP,
当P从B运动到C时,如图(1):
∵DQ=AD-AQ=16-t,
CP=21-2t
∴16-t=21-2t
解得t=5
当P从C运动到B时,
∵DQ=AD-AQ=16-t,
CP=2t-21
∴16-t=2t-21,
解得t=$\frac{37}{3}$,
∴当t=5或$\frac{37}{3}$秒时,四边形PQDC是平行四边形;
(2)若点P、Q分别沿AD、BC运动时,如图(2):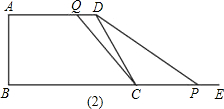
$\frac{DQ+CP}{2}•AB=60$,
即$\frac{16-t+21-2t}{2}×12=60$,
解得t=9;
若点P返回时,CP=2(t-$\frac{21}{2}$),
则$\frac{16-t+2(t-\frac{21}{2})}{2}×12=60$,
解得t=15.
故当t=9或15秒时,以C,D,Q,P为顶点的梯形面积等60cm2;
(3)当PQ=PD时,如图(3):
作PH⊥AD于H,则HQ=HD
∵QH=HD=$\frac{1}{2}$QD=$\frac{1}{2}$(16-t)
由AH=BP得2t=$\frac{1}{2}$(16-t)+t,
解得t=$\frac{16}{3}$秒;
当PQ=QD时QH=AH-AQ=BP-AQ=2t-t=t,QD=16-t,
∵QD2=PQ2=t2+122
∴(16-t)2=122+t2
解得t=$\frac{7}{2}$(秒);
当QD=PD时DH=AD-AH=AD-BP=16-2t,
∵QD2=PD2=PH2+HD2=122+(16-2t)2
∴(16-t)2=122+(16-2t)2
即3t2-32t+144=0
∵△<0,
∴方程无实根,
综上可知,当t=$\frac{16}{3}$秒或t=$\frac{7}{2}$秒时,△PQD是等腰三角形.
点评 本题主要考查了直角梯形的性质、平行四边形的性质、梯形的面积、等腰三角形的性质,特别应该注意要全面考虑各种情况,不要遗漏.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,已知线段AB∥CD,AD与BC相交于点K,∠ABC的角平线分BE交AD于E,当AE=$\frac{1}{2}$AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.
如图,已知线段AB∥CD,AD与BC相交于点K,∠ABC的角平线分BE交AD于E,当AE=$\frac{1}{2}$AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
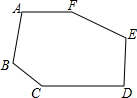 如图,六边形ABCDEF,AB∥DE,且∠A=110°,∠B=120°,∠E=100°,∠D=90°,求六边形ABCDEF其它内角的度数.
如图,六边形ABCDEF,AB∥DE,且∠A=110°,∠B=120°,∠E=100°,∠D=90°,求六边形ABCDEF其它内角的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com