
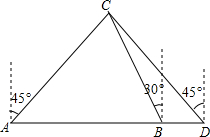
 某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里.求A、D两点间的距离.(结果不取近似值)
某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里.求A、D两点间的距离.(结果不取近似值) 分析 先作CH⊥AD,可得BD=$\frac{1}{2}$×20,AH=DH,可求AH的长,从而求得AD的长.
解答 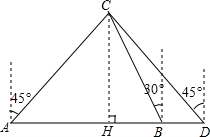 解:作CH⊥AD于点H,
解:作CH⊥AD于点H,
由题意可得:△ACD是等腰直角三角形,则CH=$\frac{1}{2}$AD,设CH=x,则DH=x,
在Rt△CBH中,∠BCH=30°,
则$\frac{BH}{CH}$=tan30°,故BH=$\frac{\sqrt{3}}{3}$x,
∴BD=x-$\frac{\sqrt{3}}{3}$x=$\frac{1}{2}$×20,
解得:x=15+5$\sqrt{3}$,
故2x=30+10$\sqrt{3}$.
答:A、D两点间的距离为(30+10$\sqrt{3}$)海里.
点评 本题考查了方向角问题,求三角形的边或高的问题一般可以转化为解直角三角形的问题,关键是作出辅助线,构造直角三角形.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:填空题
 如图,不解关于x,y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$,请直接写出它的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
如图,不解关于x,y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$,请直接写出它的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (-$\frac{1}{2}$,2) | C. | (2,-1) | D. | ($\frac{1}{2}$,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD中,AB=2,BC=3,点P是BC边上任意一点,E,F,R分别是AP,RP,CD的中点,则EF的长为( )
如图,矩形ABCD中,AB=2,BC=3,点P是BC边上任意一点,E,F,R分别是AP,RP,CD的中点,则EF的长为( )| A. | $\frac{\sqrt{13}}{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
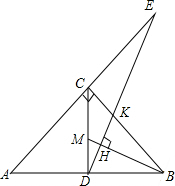 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,M是CD上的点,DH⊥BM于H,DH的延长线交AC的延长线于E.求证:
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,M是CD上的点,DH⊥BM于H,DH的延长线交AC的延长线于E.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com