
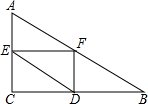
 已知:在Rt△ABC中,∠C=90°,AC=6,BC=8,点E是边AC上一动点,过点E作EF∥BC,交AB边于点F,点D为BC上任一点,连接DE,DF.设EC的长为x,则△DEF的面积y关于x的函数关系大致为( )
已知:在Rt△ABC中,∠C=90°,AC=6,BC=8,点E是边AC上一动点,过点E作EF∥BC,交AB边于点F,点D为BC上任一点,连接DE,DF.设EC的长为x,则△DEF的面积y关于x的函数关系大致为( )| A. | 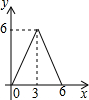 | B. | 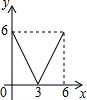 | C. | 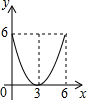 | D. | 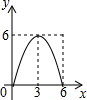 |
分析 判断出△AEF和△ABC相似,根据相似三角形对应边成比例列式求出EF,再根据三角形的面积列式表示出S与x的关系式,然后得到大致图象选择即可.
解答 解:∵EF∥BC,
∴△AEF∽△ABC,
∴$\frac{EF}{BC}=\frac{AE}{AC}$
即$\frac{EF}{8}=\frac{6-x}{6}$,
∴EF=$\frac{24-4x}{3}$,
∴S=$\frac{1}{2}$×$\frac{24-4x}{3}$•x=-$\frac{2}{3}$x2+4x=-$\frac{2}{3}$(x-3)2+6(0<x<5),
纵观各选项,只有D选项图象符合.
故选:D.
点评 本题考查了动点问题函数图象,主要利用了相似三角形的性质,求出S与x的函数关系式是解题的关键,也是本题的难点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
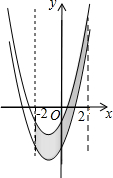 如图,已知抛物线y=x2+2x-3,把此抛物线沿y轴向上平移,平移后的抛物线和原抛物线与经过点(-2,0),(2,0)且平行于y轴的两条直线所围成的阴影部分的面积为s,平移的距离为m,则下列图象中,能表示s与m的函数关系的图象大致是( )
如图,已知抛物线y=x2+2x-3,把此抛物线沿y轴向上平移,平移后的抛物线和原抛物线与经过点(-2,0),(2,0)且平行于y轴的两条直线所围成的阴影部分的面积为s,平移的距离为m,则下列图象中,能表示s与m的函数关系的图象大致是( )| A. | 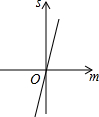 | B. | 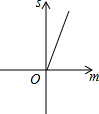 | C. | 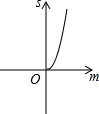 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数关系如图所示,根据图象所提供的信息解答问题:
甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数关系如图所示,根据图象所提供的信息解答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲乙两城市之间有一条公路相连,公路中途穿过丙市,现有两位司机M、N相约各自同时从甲乙两地出发,途中M将一件物品交给N,已知M从甲市到丙市,N从乙市到甲市,N的速度是M的$\frac{3}{4}$,他们开车距离丙市的距离y(千米)与行驶的时间t(小时)的函数图象如图所示.
甲乙两城市之间有一条公路相连,公路中途穿过丙市,现有两位司机M、N相约各自同时从甲乙两地出发,途中M将一件物品交给N,已知M从甲市到丙市,N从乙市到甲市,N的速度是M的$\frac{3}{4}$,他们开车距离丙市的距离y(千米)与行驶的时间t(小时)的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC和过点O的两条互相垂直的直线x、y,画出△ABC关于直线x对称的△A′B′C′,再画出△A′B′C′关于点O成中心对称的△A″B″C″.
如图,已知△ABC和过点O的两条互相垂直的直线x、y,画出△ABC关于直线x对称的△A′B′C′,再画出△A′B′C′关于点O成中心对称的△A″B″C″.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
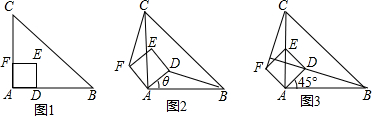
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
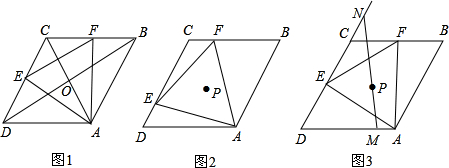
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com