
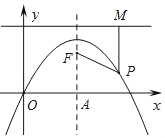
【题目】如图,抛物线y=﹣x2+2x的对称轴与x轴交于点A,点F在抛物线的对称轴上,且点F的纵坐标为![]() .过抛物线上一点P(m,n)向直线y=
.过抛物线上一点P(m,n)向直线y=![]() 作垂线,垂足为M,连结PF.
作垂线,垂足为M,连结PF.
(1)当m=2时,求证:PF=PM;
(2)当点P为抛物线上任意一点时,PF=PM是否还成立?若成立,请给出证明;若不成立,请说明理由.
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,每套西装的定价为300元,每条领带的定价为50元,厂方在开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;
②西装和领带都按定价的![]() 付款.
付款.
现某客户要到该服装厂购买西装20套,领带![]() 条(
条(![]() )
)
(1)若该客户按方案①购买,则需付款____________元(用含![]() 的代数式表示);
的代数式表示);
若该客户按方案②购买,则需付款____________元(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,则通过计算说明此时按哪种方案购买较为合算.
,则通过计算说明此时按哪种方案购买较为合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
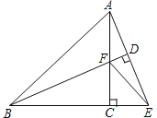
【题目】如图,在△ABC中,AC⊥BC,AC=BC,延长BC至E使BE=BA,过点B作BD⊥AE于点D,BD与AC交于点F,连接EF.
(1)求证:△ACE≌△BCF.
(2)求证:BF=2AD,
(3)若CE=![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
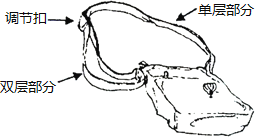
【题目】如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.乐乐用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)增长或缩短.经测量,得到如下数据:
单层部分的长度(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度(cm) | … | 73 | 72 | 71 |
| … | 0 |
(1)根据上表中数据的规律,填写表格中空白处的数据;
(2)设单层部分的长度为xcm,请用含x的代数式表示出双层部分的长度 cm;
(3)根据乐乐的身高和习惯,挎带的长度为110cm时,背起来最舒适,请求出此时单层部分的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M是BC边上一个动点,联结AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转恰好至△NGF.给出以下三个结论:①∠AND=∠MPC; ②△ABM≌△NGF;③S四边形AMFN=a2+b2.
其中正确的结论是_____(请填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样大小的两种不同颜色的正方形纸片,按图的方式拼正方形.

(1)第①个图形中有1个小正方形,第②个图形中有4个小正方形,第③个图形中有9个小正方形,第⑦个图形中有__________个小正方形.
(2)第⑩个图形比第⑨个图形多_________个小正方形.
(3)第n个图形比第n-1个图形多_________个小正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a<0)的图象与x轴的两个交点A、B的横坐标分别为﹣3、1,与y轴交于点C,下面四个结论:①16a+4b+c<0;②若P(﹣5,y1),Q(![]() ,y2)是函数图象上的两点,则y1>y2;③c=﹣3a;④若△ABC是等腰三角形,则b=﹣
,y2)是函数图象上的两点,则y1>y2;③c=﹣3a;④若△ABC是等腰三角形,则b=﹣![]() 或﹣
或﹣![]() .其中正确的有_____.(请将正确结论的序号全部填在横线上)
.其中正确的有_____.(请将正确结论的序号全部填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B、C是直径为6cm的⊙O上的点,且AB=3cm,AC=3![]() cm,则∠BAC的度数为( )
cm,则∠BAC的度数为( )
A. 15° B. 75°或15° C. 105°或15° D. 75°或105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段![]() 上.点P从点C出发向点
上.点P从点C出发向点![]() 运动,速度为2cm/s;同时,点Q也从点C以4cm/s速度出发用1s到达A处,并在A处停留2s,然后按原速度向点B运动,.最终,点Q比点P早1s到达B处.设点P运动的时间为t.
运动,速度为2cm/s;同时,点Q也从点C以4cm/s速度出发用1s到达A处,并在A处停留2s,然后按原速度向点B运动,.最终,点Q比点P早1s到达B处.设点P运动的时间为t.
(1)线段AC的长为 cm;当t=3s时,P,Q两点之间的距离为 cm;
(2)求线段BC的长;
(3)从P,Q两点同时出发至点P到达点B处的这段时间内,t为何值时,P,Q两点相距1cm?
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com