
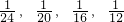 .
. ,
,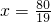 .
.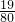 ,则n轮完成任务的
,则n轮完成任务的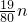 .由
.由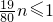 ,得
,得 ,
, .
. .
.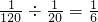 小时.
小时. 小时.
小时. 小时内完成,所以第5轮的第一个人完成余下的
小时内完成,所以第5轮的第一个人完成余下的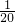 ,要至多在
,要至多在 小时内完成.
小时内完成. ,
,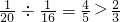 .
.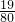 ,则2轮完成任务的
,则2轮完成任务的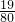 ×2,则n轮完成任务的
×2,则n轮完成任务的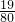 n,总工作量就是1,因此可得不等式
n,总工作量就是1,因此可得不等式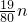 ≤1,解不等式即可得到n的最大值;然后再讨论可求出所用时间;
≤1,解不等式即可得到n的最大值;然后再讨论可求出所用时间; 小时内完成,所以第5轮的第一个人完成余下的
小时内完成,所以第5轮的第一个人完成余下的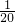 ,要至多在
,要至多在 小时内完成,根据甲、乙、丙、丁的工作效率,利用工作量÷工作效率=工作时间,计算一下哪个不能按时完成,则安排在第一位,即可得到答案.
小时内完成,根据甲、乙、丙、丁的工作效率,利用工作量÷工作效率=工作时间,计算一下哪个不能按时完成,则安排在第一位,即可得到答案.

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:竞赛题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com