
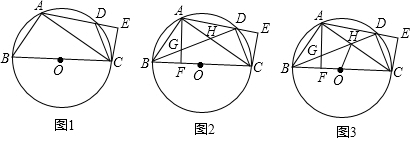
分析 (1)首先证明∠CDE=∠B,由∠B+∠ACB=90°,∠CDE+∠DCE=90°,即可推出∠DCE=∠ACB.
(2)如图2中,连接OG,延长AF交⊙O于M.首先证明OG是△BCH的中位线,再证明△OFH∽△CDH,推出$\frac{FG}{DH}$=$\frac{OG}{CH}$=$\frac{1}{2}$即可.
(3)如图3中,作OM⊥AC于M.设AG=BG=a,则BF=$\sqrt{{a}^{2}-{5}^{2}}$.由tan∠CDE=tan∠ABF=$\frac{AF}{BF}$=$\frac{3}{2}$,可得方程$\frac{a+5}{\sqrt{{a}^{2}-{5}^{2}}}$=$\frac{3}{2}$,求出a的值,想办法求出OM、HM
即可根据勾股定理解决问题.
解答 (1)证明:如图1中,
∵∠B+∠ADC=180°,∠ADC+∠CDE=180°,
∴∠CDE=∠B,
∵BC是直径,
∴∠BAC=90°,
∴∠B+∠ACB=90°,
∵CE⊥AE,
∴∠E=90°,
∴∠CDE+∠DCE=90°,
∴∠DCE=∠ACB.
(2)如图2中,连接OG,延长AF交⊙O于M.
∵OF⊥AM,
∴$\widehat{MB}$=$\widehat{AB}$=$\widehat{AD}$,
∴∠GAB=∠GBA,
∴GA=GB,
∵BC是直径,∴∠BAC=90°,
∴∠BAG+∠CAF=90°,∠AHB+∠ABG=90°,
∴∠GAH=∠GHA,
∴AG=GH,
∴BG=GH,∵BO=OC,
∴CH∥OG.CH=2OG,
∴∠GOF=∠ACB=∠DCH,∵∠OFG=∠CDH=90°,
∴△OFH∽△CDH,
∴$\frac{FG}{DH}$=$\frac{OG}{CH}$=$\frac{1}{2}$,
∴DH=2GF.
(3)如图3中,作OM⊥AC于M.设AG=BG=a,则BF=$\sqrt{{a}^{2}-{5}^{2}}$.
∵tan∠CDE=tan∠ABF=$\frac{AF}{BF}$=$\frac{3}{2}$,
∴$\frac{a+5}{\sqrt{{a}^{2}-{5}^{2}}}$=$\frac{3}{2}$,
解得a=13或5(舍弃),
∴AG=BG=GH=13,
在Rt△BGF中,BF=$\sqrt{B{G}^{2}-F{G}^{2}}$=12,
在Rt△ABF中,AB=$\sqrt{A{F}^{2}+B{F}^{2}}$=$\sqrt{1{2}^{2}+1{8}^{2}}$=6$\sqrt{13}$,
在Rt△ABH中,AH=$\sqrt{B{H}^{2}-A{B}^{2}}$=$\sqrt{2{6}^{2}-(6\sqrt{13})^{2}}$=4$\sqrt{13}$,
∵AF2=FB•FC,
∴FC=27,
∴BC=BF+FC=12+27=39,
在Rt△ACB中,AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{3{9}^{2}-(6\sqrt{13})^{2}}$=9$\sqrt{13}$,
∴CH=AC-AH=5$\sqrt{13}$,
∵OM⊥AC,
∴OM=CM=4.5$\sqrt{13}$,
∴HM=$\frac{1}{2}$$\sqrt{13}$,
∵OB=OC,CM=MA,
∴OM=$\frac{1}{2}$AB=3$\sqrt{13}$,
在Rt△OMH中,OH=$\sqrt{O{M}^{2}+H{M}^{2}}$=$\sqrt{(3\sqrt{13})^{2}+(\frac{1}{2}\sqrt{13})^{2}}$=$\frac{\sqrt{481}}{2}$.
点评 本题考查圆综合题、垂径定理、圆周角定理、勾股定理、相似三角形的判定和性质、锐角三角函数、三角形的中位线定理等知识,解题的关键是灵活运用所学知识解决问题,学会用方程的思想思考问题,学会利用相似三角形的性质解决线段之间的关系问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
 如图,是由每个边长都是1的小正方形构成的网格,点O,A,B,M均为格点,P为线段OM上的一个动点.
如图,是由每个边长都是1的小正方形构成的网格,点O,A,B,M均为格点,P为线段OM上的一个动点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
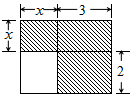 下面四个整式中,不能表示图中阴影部分面积的是( )
下面四个整式中,不能表示图中阴影部分面积的是( )| A. | (x+3)(x+2)-2x | B. | x(x+3)+6 | C. | 3(x+2)+x2 | D. | x2+5x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-2(x-1)2+6 | B. | y=-2(x-1)2-6 | C. | y=-2(x+1)2+6 | D. | y=-2(x+1)2-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解一批圆珠笔的使用寿命 | |
| B. | 了解全国八年级学生身高的现状 | |
| C. | 检查发射神舟11号飞船的运载火箭的各零部件 | |
| D. | 考察世界人们保护海洋的意识 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com