
【题目】如图,边长为2的正方形ABCD内接于⊙O,点E是 ![]() 上一点(不与A、B重合),点F是
上一点(不与A、B重合),点F是 ![]() 上一点,连接OE,OF,分别与AB,BC交于点G,H,有下列结论:
上一点,连接OE,OF,分别与AB,BC交于点G,H,有下列结论:
① ![]() =
= ![]() ;
;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④若BG=1﹣ ![]() ,则BG,GE,
,则BG,GE, ![]() 围成的面积是
围成的面积是 ![]() +
+ ![]() .
.
其中正确的是(把所有正确结论的序号都填上)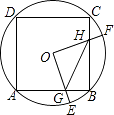
【答案】①②
【解析】如图所示,连接OC、OB、CF、BE.
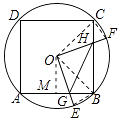
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
∴ ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ;故①正确,
;故①正确,
在△BOG与△COH中,
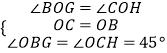 ,
,
∴△BOG≌△COH(ASA),
∴OG=OH,
∵∠HOG=90°
∴△OGH是等腰直角三角形,②正确,
∴S△OBG=S△OCH,
∴S四边形OGBH=S△BOC= ![]() S正方形ABCD=定值,故③错误;
S正方形ABCD=定值,故③错误;
作OM⊥AB于M,则OM=BM= ![]() AB=1,OB=
AB=1,OB= ![]() OM=
OM= ![]() ,
,
∴GM= ![]() ,
,
∴tan∠GOM= ![]() =
= ![]() ,
,
∴∠GOM=30°,
∵∠BOM=45°,
∴∠BOG=45°﹣30°=15°,
∴扇形BOE的面积= ![]() =
= ![]() ,
,
∵BG=1﹣ ![]() ,
,
∴AG=1+ ![]() ,
,
过G作GP⊥BO于P,
∴PG=PB= ![]() ﹣
﹣ ![]() ,
,
∴△OBG的面积= ![]() ×
× ![]() ×(
×( ![]() ﹣
﹣ ![]() )=
)= ![]() ﹣
﹣ ![]() ,
,
∴BG,GE, ![]() 围成的面积=扇形BOE的面积﹣△BOG的面积=
围成的面积=扇形BOE的面积﹣△BOG的面积= ![]() ﹣
﹣ ![]() +
+ ![]() ,故④错误.
,故④错误.
所以答案是:①②.
【考点精析】根据题目的已知条件,利用正多边形和圆和扇形面积计算公式的相关知识可以得到问题的答案,需要掌握圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).


科目:初中数学 来源: 题型:
【题目】(1)阅读下面的材料并把解答过程补充完整.
问题:在关于![]() ,
,![]() 的二元一次方程组
的二元一次方程组![]() 中,
中,![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
在关于![]() ,
,![]() 的二元一次方程组中,利用参数
的二元一次方程组中,利用参数![]() 的代数式表示
的代数式表示![]() ,
,![]() ,然后根据
,然后根据![]() ,
,![]() 列出关于参数
列出关于参数![]() 的不等式组即可求得
的不等式组即可求得![]() 的取值范围.解:由
的取值范围.解:由![]() ,解得
,解得 ,又因为
,又因为![]() ,
,![]() ,所以
,所以 解得____________.
解得____________.
(2)请你按照上述方法,完成下列问题:
①已知![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
②已知![]() ,在关于
,在关于![]() ,
,![]() 的二元一次方程组
的二元一次方程组![]() 中,
中,![]() ,
,![]() ,请直接写出
,请直接写出![]() 的取值范围(结果用含
的取值范围(结果用含![]() 的式子表示)____________.
的式子表示)____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)x(﹣x)2(﹣x)3;(2)x3x5﹣(2x4)2+x10÷x2.
(3)(﹣0.125)2018×82019;(4)(a﹣b)10÷(b﹣a)3÷(b﹣a)3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AD=BD=BC.在BC延长线上取点C1,连接DC1,使DC=CC1,在CC1延长线上取点C2,在DC1上取点E,使EC1=C1C2,同理FC2=C2C3,若继续如此下去直到Cn,则∠Cn的度数为____.(结果用含![]() 的代数式表示)
的代数式表示)
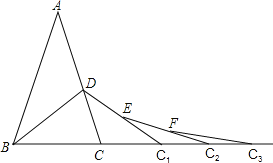
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于 ![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M. 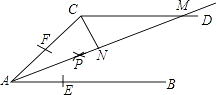
(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,若AB∥CD,将点P在AB、CD内部,∠B,∠D,∠P满足的数量关系是 ,并说明理由.
(2)在图1中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图2,利用(1)中的结论(可以直接套用),求∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?
(3)科技活动课上,雨轩同学制作了一个图(3)的“飞旋镖”,经测量发现∠PAC=30°,∠PBC=35°,他很想知道∠APB与∠ACB的数量关系,你能告诉他吗?说明理由.
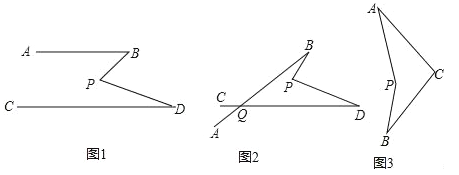
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数 y=kx+4(k≠0).
(1)当 x=-1 时,y=2,求此函数的表达式;
(2)函数图象与 x 轴、y 轴的交点分别为 A、B, 求出△AOB 的面积;
(3)利用图象求出当 y≤3 时,x 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 . 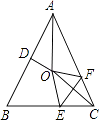
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com