考点:解一元二次方程-因式分解法,解一元二次方程-配方法,解一元二次方程-公式法
专题:计算题
分析:(1)方程移项后,分解因式化为积的形式,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(2)找出a,b,c的值,计算出根的判别式大于0,代入求根公式即可求出解;
(3)找出a,b,c的值,计算出根的判别式大于0,代入求根公式即可求出解;
(4)将x-2看做一个整体,移项后,利用完全平方公式分解,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
解答:解:(1)方程移项得:x
2-8x-20=0,
分解因式得:(x+2)(x-10)=0,
解得:x
1=-2,x
2=10;
(2)这里a=2,b=-6,c=-1,
∵△=36+8=44,
∴x=
=
;
(3)方程变形得:
x
2-4x-4
=0,
这里a=
,b=-4,c=-4
,
∵△=16+16=32,
∴x=
=
±2;
(4)方程变形得:(x-2)
2-4(x-2)+4=0,
分解因式得:(x-2-2)
2=0,
解得:x
1=x
2=4.
点评:此题考查了解一元二次方程-因式分解法,公式法,以及配方法,熟练掌握各自解法是解本题的关键.



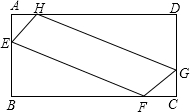 为了美化校园环境,某校准备在一块空地(如图所示的长方形ABCD,AB=10m,BC=20m)上进行绿化,中间的一块(图中四边形EFGH)上种花,其他的四块(图中的四个直角三角形)上铺设草坪,并要求AE=AH=CF=CG,那么在满足上述条件的所有设计中,是否存在一种设计,使得四边形EFGH的面积最大?
为了美化校园环境,某校准备在一块空地(如图所示的长方形ABCD,AB=10m,BC=20m)上进行绿化,中间的一块(图中四边形EFGH)上种花,其他的四块(图中的四个直角三角形)上铺设草坪,并要求AE=AH=CF=CG,那么在满足上述条件的所有设计中,是否存在一种设计,使得四边形EFGH的面积最大? 如图,已知反比例函数y1=
如图,已知反比例函数y1=