
 先阅读理解下面的例题,再按要求解答下列问题:
先阅读理解下面的例题,再按要求解答下列问题:分析 (1)直接根据阅读材料,求得所求代数式的最小值;
(2)根据阅读材料可以将求所求的式子转化为材料中的形式,从而可以求得所求代数式的最小值;
(3)根据意义,可以列出相应的代数式,然后化为材料中的形式,从而可以求得所求面积的最大值.
解答 解:(1)(x-1)2+5,
∵(x-1)2≥0,
∴(x-1)2+5≥5,
即代数式(x-1)2+5的最小值是5;
(2)m2+2m+4=(m+1)2+3,
∵(m+1)2≥0,
∴(m+1)2+3≥3,
即代数式m2+2m+4的最小值是3;
(3)由题意可得,
花园的面积为:x(20-2x)=-2x2+20x=-2(x2-10x)=-2(x-5)2+50,
∴当x=5时,花园的面积取得最大值,此时花园的面积是50,BC的长是20-2×5=10<15,
即当x取5时,花园的面积最大,最大面积是50m2.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:选择题
 如图,一斜坡上栽树,相邻在坡面上的距离AB=13m,水平距离为12m,则该斜坡坡度i为( )
如图,一斜坡上栽树,相邻在坡面上的距离AB=13m,水平距离为12m,则该斜坡坡度i为( )| A. | 5:12 | B. | 12:13 | C. | 12:5 | D. | 1:$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 用一个平面去截一个正方体可能截得五边形 | |
| B. | 五棱柱有10个顶点 | |
| C. | 沿直角三角形某条边所在的直线旋转一周,所得的几何体为圆柱 | |
| D. | 将折起的扇子打开,属于“线动成面”的现象 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
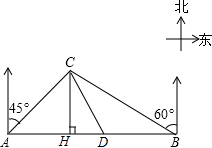 川西某高原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.
川西某高原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{4\frac{1}{4}}$=2$\frac{1}{2}$ | D. | $\sqrt{(-3)^{2}}$=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com