
 对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|叫做P1、P2两点间的直角距离,记作d(P1,P2).
对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|叫做P1、P2两点间的直角距离,记作d(P1,P2).分析 (1)根据题中所给出的两点的直角距离公式即可得出结论;
(2)根据坐标原点O点坐标为(0,0),再由两点的直角距离公式即可得出结论;
(3)先根据题意得出关于x的式子,再由绝对值的几何意义即可得出结论.
解答 解:(1)∵P1(1,-2)、Q1(-3,4)
∴P1、Q1两点的直角距离为d(P1,Q1)=|1+3|+|-2-4|=10,
(2)∵坐标原点O点坐标为(0,0),动点P(x,y)满足d(O,P)=1,
∴|0-x|+|0-y|=1,
即|x|+|y|=1.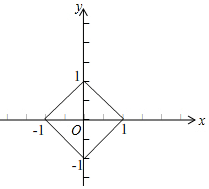
(3)∵Q(x,y)是直线y=x+2上的动点,M(2,1),
∴Q(x,x+2),
∴d(M,Q)=|2-x|+|1-(x+2)|=|2-x|+|-1-x|=|x-2|+|x+1|,
∵|x-2|+|x+1|表示数轴上实数x所对应的点到-1和2所对应的点的距离之和,其最小值为3.
∴点M(2,1)到直线y=x+2的直角距离是3.
点评 此题主要考查了一次函数图象,涉及的知识有:绝对值的代数意义,弄清题中的新定义是解本题的关键


科目:初中数学 来源: 题型:解答题
 如图,抛物线顶点坐标为点C(2,8),交x轴于点A(6,0),交y轴于点B.
如图,抛物线顶点坐标为点C(2,8),交x轴于点A(6,0),交y轴于点B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-5,0),对称轴为直线x=-2,给出四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-5,0),对称轴为直线x=-2,给出四个结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
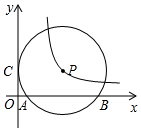 如图,⊙P与y轴相切于点C(0,3),与x轴相交于点A(1,0),B(9,0).双曲线y=$\frac{k}{x}$恰好经过圆心P,那么k的值是15.
如图,⊙P与y轴相切于点C(0,3),与x轴相交于点A(1,0),B(9,0).双曲线y=$\frac{k}{x}$恰好经过圆心P,那么k的值是15.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
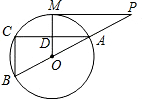 如图,MP切⊙O于点M,直线PO交⊙O于点A、B,弦AC∥MP,交OM于点D.
如图,MP切⊙O于点M,直线PO交⊙O于点A、B,弦AC∥MP,交OM于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-3)2=9 | B. | (x-3)2=13 | C. | (x+3)2=5 | D. | (x-3)2=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2).
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,OD、OE分别为∠AOC、∠COB的平分线,则∠AOB和∠DOE的关系是( )
如图,OD、OE分别为∠AOC、∠COB的平分线,则∠AOB和∠DOE的关系是( )| A. | $\frac{1}{3}$∠AOB=∠DOE | B. | ∠AOB=2∠DOE | C. | 互补 | D. | 互余 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com