【题目】已知点C为直径BA的延长线上一点，CD切⊙O于点D，
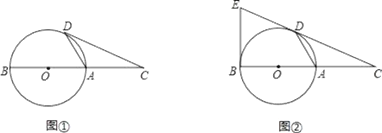
（Ⅰ）如图①，若∠CDA=26°，求∠DAB的度数；
（Ⅱ）如图②，过点B作⊙O的切线交CD的延长线于点E，若⊙O的半径为3，BC=10，求BE的长．
【答案】(I)∠DAB =64°；(II) BE的长是
【解析】
（I）根据切线的性质得出∠ODC=90°，求出∠ODA，根据等腰三角形的性质求出即可；
（II）根据切线长定理得出BE=DE，根据勾股定理求出DC，根据勾股定理得出方程，求出方程的解即可．
(I)如图①，连接OD，
∵CD切⊙O于点D，
∴∠ODC=90°，
∴∠CDA+∠ODA=90°，
∵∠CDA=26°，
∴∠ADO=64°，
∵OD=OA，
∴∠DAB=∠ODA=64°；
(II)如图②，连接OD，
在Rt△ODC中，OC=BCOB=103=7，
∵ED、EB分别为⊙O的切线，
∴ED=EB，
在Rt△CBE中，设BE=x，由
得：
解得：
∴BE的长是
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD是矩形，把矩形沿AC折叠，点B落在点E处，AE与DC的交点为O，连接DE．
（1）求证：△ADE≌△CED；
（2）求证：DE∥AC．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系 xOy 中，将点 A（2，4）向下平移 2 个单位得到点 C，反比例函数y 
(m≠0)的图象经过点 C，过点 C 作 CB⊥x 轴于点 B
（1）求 m 的值；
（2）一次函数 y=kx+b(k<0)的图象经过点 C，交 x 轴于点 D， 线段 CD，BD，BC 围成的区域（不含边界）为 G； 若横、纵坐标都是整数的点叫做整点
①b=3 时，直接写出区域 G 内的整点个数
②若区域 G 内没有整点，结合函数图象，确定 k 的取值范围
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
内部做
，
平分，
，
，
，点
为
的中点：动点
由
出发，沿运动，速度为每秒5个单位，动点
由出发，沿
运动，速度为每秒8个单位，当点到达点
时，两点同时停止运动；过、、作
；
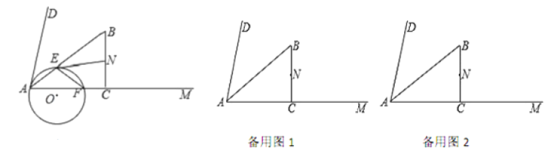
（1）判断
的形状为________，并判断
与的位置关系为__________；
（2）求
为何值时，
与相切？求出此时的半径，并比较半径与劣弧
长度的大小；
（3）直接写出的内心运动的路径长为__________；（注：当、、重合时，内心就是点）
（4）直接写出线段与有两个公共点时，的取值范围为__________．
（参考数据：
，
，
，
，
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：规定max（a，b）＝
，例如：max（﹣1，2）＝2，max（3，3）＝3．
感知：已知函数y＝max（x+1，﹣2x+4）
（1）当x＝3时，y＝_____；
（2）当y＝3时，x＝______；
（3）当y随x的增大而增大时，x的取值范围为______；
（4）当﹣1≤x≤4时，y的取值范围为______；
探究：已知函数y＝max（x+2，
）当直线y＝m（m为常数）与函数y＝max（x+2，）（﹣6＜x≤3）的图象有两个公共点时，m的取值范围为_______；
拓展：已知函数y＝max（﹣x2+2nx，﹣nx）（n为常数且n≠0），当
n﹣3≤x≤2时，随着x的增大，函数值y先减小后增大，直接写出n的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
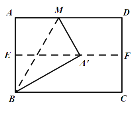
【题目】如图，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平，再一次折叠纸片，使点A落在EF上的点A′处，并使折痕经过点B，得到折痕BM，若矩形纸片的宽AB=4，则折痕BM的长为( )
A.
B.
C.8D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知
，当
时，
．
（1）求这个函数的表达式；
（2）在给出的平面直角坐标系中，请用你喜欢的方法画出这个函数的图象并写出这个函数的一条性质；
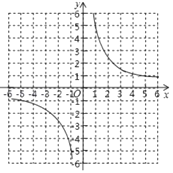
（3）已知函数
的图象如图所示，结合你所画的函数图象，直接写出不等式
的解集．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
