
阅读并回答问题:
小亮是一位刻苦学习、勤于思考、勇于创新的同学.一天他在解方程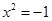 时,突发
时,突发
奇想: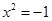 在实数范围内无解,如果存在一个数i,使
在实数范围内无解,如果存在一个数i,使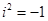 ,那么当
,那么当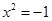 时,有
时,有
 i,从而
i,从而 i是方程
i是方程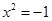 的两个根.
的两个根.
据此可知:
1. i可以运算,例如:i3=i2·i=-1×i=-i,则i4= ,
i2011=______________,i2012=__________________;
2.方程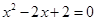 的两根为
(根用i表示).
的两根为
(根用i表示).
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| b |
| a |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| 2a |
| b |
| a |
| c |
| a |
| b |
| 2a |
| b |
| 2a |
| b2-4ac |
| 4a2 |
| b |
| 2a |
|
-b±
| ||
| 2a |
-b+
| ||
| 2a |
-b-
| ||
| 2a |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
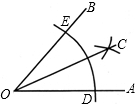 |
作法:①在OA,OB上分别截取OD,OE,使OD=OE. ②分别以D,E为圆心,以大于
两弧在∠AOB内交于点C. ③作射线OC,则OC就是∠AOB的平分线 |
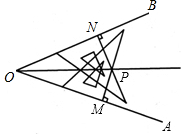 |
作法:①利用三角板上的刻度,在OA,OB上分别截取OM,ON,使OM=ON. ②分别过以M,N为OM,ON的垂线,交于点P. ③作射线OP,则OP就是∠AOB的平分 线. |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 2 |
| x+1 |
| 3 |
| x-1 |
| 1 |
| x2-1 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com