练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．小芳家房屋装修时，选中了一种漂亮的正八边形地砖．建材店老板告诉她，只用一种八边形地砖是不能密铺地面的，便向她推荐了几种形状的地砖．你认为要使地面密铺，小芳应选择另一种形状的地砖是（　　）
    A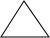．B．C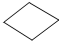．D．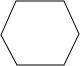

    分析 正八边形的一个内角为135°，从所给的选项中取出一些进行判断，看其所有内角和是否为360°，并以此为依据进行求解．

    解答 解：A、正八边形、正三角形内角分别为135°、60°，显然不能构成360°的周角，故不能铺满；
    B、正方形、八边形内角分别为90°、135°，由于135×2+90=360，故能铺满；
    C、正八边形的内角为135°，菱形的内角度数不确定，所以不一定能构成360°的周角，故不能铺满；
    D、正六边形和正八边形内角分别为120°、135°，显然不能构成360°的周角，故不能铺满；
    故选B．

    点评 本题考查平面镶嵌（密铺），解决此类题，可以记住几个常用正多边形的内角，及能够用两种正多边形镶嵌的几个组合．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    10．已知点P（-2，4）与点Q关于原点对称，那么点Q的坐标是（2，-4）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

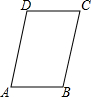    11．如图，已知四边形ABCD是平行四边形．
    （1）作∠A的平分线交BC于点E．（用尺规作图，保留作图痕迹，不用写作法）
    （2）在（1）中，若AD=6，EC=2，求平行四边形ABCD的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．某班级为筹备新年的联欢会，班长对全班学生爱吃哪几种水果作了民意调查，那么最终买什么水果，下面调查数据中最值得关注的是（　　）
    A．众数B．平均数C．中位数D．加权平均数

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．计算：$\sqrt{2\frac{14}{25}}$=$\frac{8}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列说法中不正确的是（　　）
    A．线段有1条对称轴
    B．等边三角形有3条对称轴
    C．角只有1条对称轴
    D．底与腰不相等的等腰三角形只有一条对称轴

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．甲、乙两人在相同的条件下，各射靶10次，经过计算：甲、乙的平均数均是7，甲的方差是1.2，乙的方差是5.8，下列说法中不正确的是（　　）
    A．甲、乙射中的总环数相同B．甲、乙的众数相同
    C．乙的成绩波动较大D．甲的成绩稳定

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．菱形的两条对角线长分别为2和2$\sqrt{3}$，则该菱形的高为$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．在图中，∠1和∠2是对顶角的是（　　）
    A．B．C．D．

    查看答案和解析>>

    同步练习册答案