
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
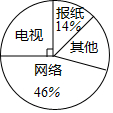 小明为了解他所居住小区居民最近“接受信息的最主要渠道”,利用课余时间,问卷调查了他所居住小区的居民,数据整理后,绘制成如下的扇形统计图.如果填写“接受信息的最主要渠道”是“网络”的人数有276名,试问:
小明为了解他所居住小区居民最近“接受信息的最主要渠道”,利用课余时间,问卷调查了他所居住小区的居民,数据整理后,绘制成如下的扇形统计图.如果填写“接受信息的最主要渠道”是“网络”的人数有276名,试问:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
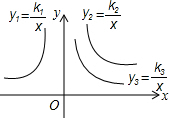 如图,是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )
如图,是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )| A. | k1>k2>k3 | B. | k3>k1>k2 | C. | k2>k3>k1 | D. | k3>k2>k1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com