
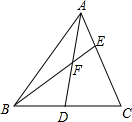
 已知如图,F为AD的中点,$\frac{AE}{EC}$=$\frac{1}{2}$,求$\frac{BD}{CD}$和$\frac{BF}{FE}$.
已知如图,F为AD的中点,$\frac{AE}{EC}$=$\frac{1}{2}$,求$\frac{BD}{CD}$和$\frac{BF}{FE}$. 分析 过A作AG∥BC,交BE的延长线于G,根据平行线分线段成比例定理,即可得到BD=AG,BC=2AG,即可得到$\frac{BD}{CD}$的值;根据平行线分线段成比例定理,得到BF=$\frac{1}{2}$BG,EF=$\frac{1}{6}$BG,即可得出$\frac{BF}{FE}$的值.
解答 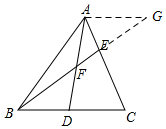 解:如图,过A作AG∥BC,交BE的延长线于G,
解:如图,过A作AG∥BC,交BE的延长线于G,
∵F为AD的中点,
∴$\frac{AG}{DB}$=$\frac{AF}{DF}$=1,
即BD=AG,
∵$\frac{AG}{CB}$=$\frac{AE}{CE}$=$\frac{1}{2}$,
∴BC=2AG,
∴CD=BD,
∴$\frac{BD}{CD}$=1;
∵AG∥BC,
∴$\frac{GE}{BE}$=$\frac{AE}{CE}=\frac{1}{2}$,
∴BE=$\frac{2}{3}$BG,
又∵$\frac{GF}{BF}=\frac{AF}{DF}=1$,
∴BF=$\frac{1}{2}$BG,
∴EF=BE-BF=$\frac{2}{3}$BG-$\frac{1}{2}$BG=$\frac{1}{6}$BG,
∴$\frac{BF}{FE}$=$\frac{\frac{1}{2}BG}{\frac{1}{6}BG}$=3.
点评 本题主要考查了平行线分线段成比例定理的运用,解决问题的关键是作辅助线构造相似三角形.平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:选择题
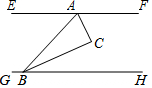 如图,Rt△ABC的锐角顶点A、B分别在直线EF、GH上,且EF∥GH,若∠CAF=65°,则∠CBH的度数为( )
如图,Rt△ABC的锐角顶点A、B分别在直线EF、GH上,且EF∥GH,若∠CAF=65°,则∠CBH的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>0 | B. | y1>0>y2 | C. | 0>y1>y2 | D. | y2>0>y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
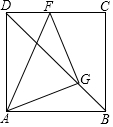 如图,边长为4的正方形ABCD,F是边DC上一点,射线AF顺时针旋转45°,交对角线BD于点G.
如图,边长为4的正方形ABCD,F是边DC上一点,射线AF顺时针旋转45°,交对角线BD于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
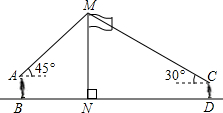 如图,某数学兴趣小组在活动课上测量学校旗杆高度,已知小明的眼睛与地面的距离AB是1.7m,看旗杆顶部M的仰角为45°,小红的眼睛与地面的距离CD是1.5m,看旗杆顶部M的仰角为30°.两人相距23m且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.【参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,结果保留整数】
如图,某数学兴趣小组在活动课上测量学校旗杆高度,已知小明的眼睛与地面的距离AB是1.7m,看旗杆顶部M的仰角为45°,小红的眼睛与地面的距离CD是1.5m,看旗杆顶部M的仰角为30°.两人相距23m且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.【参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,结果保留整数】查看答案和解析>>
科目:初中数学 来源: 题型:填空题
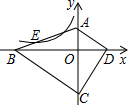 如图,四边形ABCD的顶点都在坐标轴上,若AD∥BC,△ACD与△BCD的面积分别为10和20,若双曲线y=$\frac{k}{x}$恰好经过边AB的四等分点E(BE<AE),则k的值为-$\frac{5}{2}$.
如图,四边形ABCD的顶点都在坐标轴上,若AD∥BC,△ACD与△BCD的面积分别为10和20,若双曲线y=$\frac{k}{x}$恰好经过边AB的四等分点E(BE<AE),则k的值为-$\frac{5}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com