
【题目】如图,已知 ![]() ,
, ![]() .
.
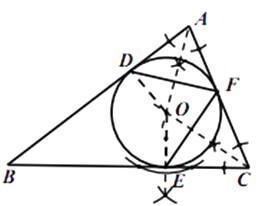
(1)在图中,用尺规作出 ![]() 的内切圆
的内切圆 ![]() ,并标出
,并标出 ![]() 与边
与边 ![]() ,
, ![]() ,
, ![]() 的切点
的切点 ![]() ,
, ![]() ,
, ![]() (保留痕迹,不必写作法);
(保留痕迹,不必写作法);
(2)连接 ![]() ,
, ![]() ,求
,求 ![]() 的度数.
的度数.
【答案】
(1)
如图,圆O即可所求。
(2)
解:连结OD,OE,则OD⊥AB,OE⊥BC,
所以∠ODB=∠OEB=90°,又因为∠B=40°,
所以∠DOE=140°,
所以∠EFD=70°.
【解析】(1)用尺规作图的方法,作出∠A和∠C的角平分线的交点即为内切圆O;
(2)由切线的性质可得∠ODB=∠OEB=90°,已知∠B的度数,根据四边形内角和360度,可求得∠DOE,由圆周角定理可求得∠EFD.
【考点精析】解答此题的关键在于理解圆周角定理的相关知识,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半,以及对切线的性质定理的理解,了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分别直方图和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图
(2)求扇形统计图中m的值和E组对应的圆心角度数
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.
(1)如图1,AC:AB=1:2,EF⊥CB,求证:EF=CD. 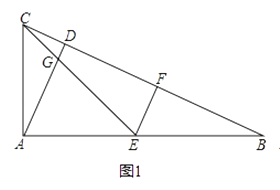
(2)如图2,AC:AB=1: ![]() ,EF⊥CE,求EF:EG的值.
,EF⊥CE,求EF:EG的值. 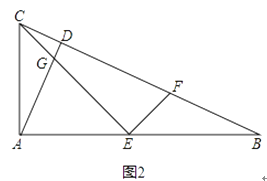
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于函数 ![]() 的四个命题:①当
的四个命题:①当 ![]() 时,
时, ![]() 有最小值10;②
有最小值10;② ![]() 为任意实数,
为任意实数, ![]() 时的函数值大于
时的函数值大于 ![]() 时的函数值;③若
时的函数值;③若 ![]() ,且
,且 ![]() 是整数,当
是整数,当 ![]() 时,
时, ![]() 的整数值有
的整数值有 ![]() 个;④若函数图象过点
个;④若函数图象过点 ![]() 和
和 ![]() ,其中
,其中 ![]() ,
, ![]() ,则
,则 ![]() .其中真命题的序号是( )
.其中真命题的序号是( )
A.①
B.②
C.③
D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数 ![]() (
( ![]() )与反比例函数
)与反比例函数 ![]() (
( ![]() )的图象交于点
)的图象交于点 ![]() ,
, ![]() .
.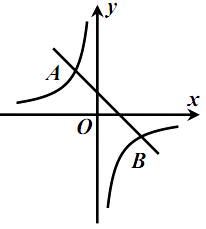
(1)求这两个函数的表达式;
(2)在 ![]() 轴上是否存在点
轴上是否存在点 ![]()
![]() ,使
,使 ![]() 为等腰三角形?若存在,求
为等腰三角形?若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观潮信息如表:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离 ![]() (千米)与时间
(千米)与时间 ![]() (分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点 ![]() ,点
,点 ![]() 坐标为
坐标为 ![]() ,曲线
,曲线 ![]() 可用二次函数
可用二次函数 ![]() (
( ![]() ,
, ![]() 是常数)刻画.
是常数)刻画.
(1)求 ![]() 的值,并求出潮头从甲地到乙地的速度;
的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以 ![]() 千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为 ![]() 千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度 ![]() ,
, ![]() 是加速前的速度).
是加速前的速度).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的条件是( )
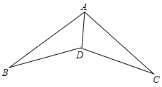
A. ∠B=∠C,BD=DC B. ∠ADB=∠ADC,BD=DC
C. ∠B=∠C,∠BAD=∠CAD D. BD=DC,AB=AC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com