

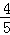 (3)
(3)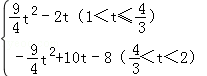
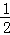 DP=
DP=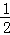 AP=
AP=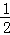 t.
t.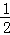 t+t=2,解得:t=
t+t=2,解得:t=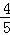 .
.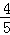 .
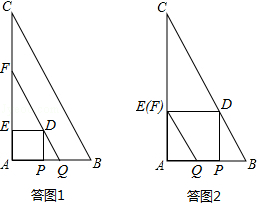
.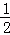 t,求得t=
t,求得t= s,进一步分析可知此时点E与点F重合;
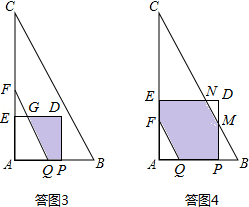
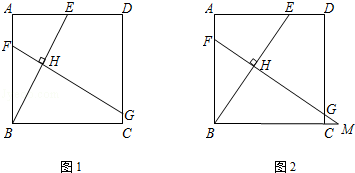
s,进一步分析可知此时点E与点F重合; 时,如答图3所示,此时重合部分为梯形PDGQ.
时,如答图3所示,此时重合部分为梯形PDGQ.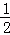 EF=2﹣
EF=2﹣ t,
t, t)=
t)= t﹣2.
t﹣2. (PQ+DG)•PD=
(PQ+DG)•PD= [(2t﹣2)+(
[(2t﹣2)+( t﹣2)]•t=
t﹣2)]•t=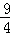 t2﹣2t;
t2﹣2t;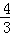 <t<2时,如答图4所示,此时重合部分为一个多边形.
<t<2时,如答图4所示,此时重合部分为一个多边形. (3t﹣4).
(3t﹣4). AQ•AF﹣
AQ•AF﹣ DN•DM
DN•DM (2﹣t)(4﹣2t)﹣
(2﹣t)(4﹣2t)﹣ ×
× (3t﹣4)×(3t﹣4)
(3t﹣4)×(3t﹣4) t2+10t﹣8.
t2+10t﹣8.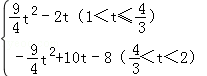 .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 =
=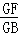 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
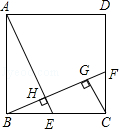
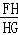 = _________ ;
= _________ ;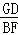 的值;
的值;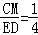 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ABC分成面积相等的两部分,即SⅠ=SⅡ,求AD的长.
ABC分成面积相等的两部分,即SⅠ=SⅡ,求AD的长.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
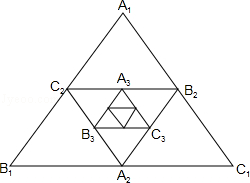
A. | B.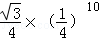 | C.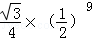 | D.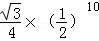 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com