
 如图,在直角∠O的内部有一滑动杆AB=10cm,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动.
如图,在直角∠O的内部有一滑动杆AB=10cm,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动.分析 根据直角三角形斜边上的中线等于斜边的一半得到OC=$\frac{1}{2}$AB=$\frac{1}{2}$A′B′=OC′,从而得出滑动杆的中点C所经过的路径是一段圆弧.
解答 解:连接OC、OC′,如图,
∵∠AOB=90°,C为AB中点,
∴OC=$\frac{1}{2}$AB=$\frac{1}{2}$A′B′=OC′,
∴当端点A沿直线AO向下滑动时,AB的中点C到O的距离始终为定长,
∴滑动杆的中点C所经过的路径是一段圆弧.
故选B
∵AB=10cm,
∴滑动杆的中点C所经过的路径的长度为$\frac{90•π•5}{180}$=2.5πcm.
点评 本题考查了轨迹,圆的定义与性质,掌握直角三角形斜边上的中线等于斜边的一半是解题的关键.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:解答题
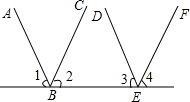 完成下列推理说明:
完成下列推理说明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △ABC是⊙O的内接三角形,BC=$\sqrt{3}$.如图,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA=$\frac{1}{2}$BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由.
△ABC是⊙O的内接三角形,BC=$\sqrt{3}$.如图,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA=$\frac{1}{2}$BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图矩形ABCD中,E为BC上一点,DF⊥AE于点F.
如图矩形ABCD中,E为BC上一点,DF⊥AE于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:点C在线段AE上,线段AC=6,线段CE=4,点B、D分别是AC、CE的中点,求线段BD的长度.
已知:点C在线段AE上,线段AC=6,线段CE=4,点B、D分别是AC、CE的中点,求线段BD的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是一个按照某种规律排列的正整数数阵
如图是一个按照某种规律排列的正整数数阵查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com