
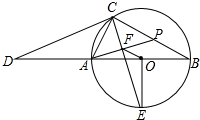
分析 (1)先利用直角三角形的两锐角互余和对顶角,得出∠BAP=∠OEG,再用同弧所对的圆周角相等得出∠ABC=∠AEC,最后用三角形的外角得出∠APC=∠AEO=45°即可;
(2)先利用切线的性质得出∠AOC=60°,进而得出∠BAC=60°,再利用锐角三角函数求出BC,进而得出BP,最后利用三角形的中位线判断出OF=$\frac{1}{2}$BP即可.
解答 解:(1)如图1,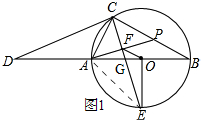
连接AE,
∵OE⊥AB,
∴∠AOE=90°,∠AEO=45°,
∴∠OEG+∠OGE=90°,
∵AF⊥CE,
∴∠AFG=90°,
∴∠FAG+∠AGF=90°,
∵∠AGF=∠OGE,
∴∠OEG=∠BAP,
∵∠AEC=∠ABC,
∴∠APC=∠ABC+∠BAP=∠AEC+∠OEG=∠AEO=45°,
∵AB是⊙O直径,
∴∠ACB=90°,
∴∠BAC=90°-∠APC=45°=∠APC,
∴CA=CP;
(2)如图2,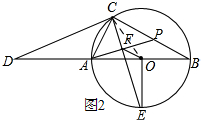
连接OC,
∵CD是⊙O的切线,
∴∠DCO=90°,
∵∠D=30°,
∴∠AOC=60°,
∵OA=OC,
∴∠BAC=60°
在Rt△ABC中,AC=$\sqrt{3}$,
∴BC=ACtan∠BAC=ACtan60°=$\sqrt{3}$×$\sqrt{3}$=3,
由(1)知,CP=AC=$\sqrt{3}$,
∴BP=BC-CP=3-$\sqrt{3}$,
由(1)知AC=CP,
∵AF⊥CE,
∴AF=PF,
∵OA=OB,
∴OF=$\frac{1}{2}$BP=$\frac{1}{2}$(3-$\sqrt{3}$).
点评 此题是切线的性质,主要考查了圆的性质,直角三角形的性质,三角形的中位线,圆周角的性质,求出∠APC=45°,和求出∠BAC=60°是解本题的关键.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:选择题
 如图,在正方形ABCD中,AB=1,连接AC,以AC为边作第一个正方形ACC1D1,连接AC1,以AC1为边作第二个正方形AC1C2D2,则第10个正方形边长为( )
如图,在正方形ABCD中,AB=1,连接AC,以AC为边作第一个正方形ACC1D1,连接AC1,以AC1为边作第二个正方形AC1C2D2,则第10个正方形边长为( )| A. | 8 | B. | 16 | C. | 32 | D. | 64 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
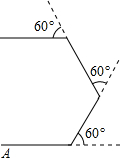 如图,小明从点A出发,沿直线前进8m后向左转60°,再沿直线前进8m,又向左转60°…照这样走下去,小明第一次回到出发点A,一共走了48米.
如图,小明从点A出发,沿直线前进8m后向左转60°,再沿直线前进8m,又向左转60°…照这样走下去,小明第一次回到出发点A,一共走了48米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-x2+2x+3 | B. | y=x2-2x+3 | C. | y=x2+2x+3 | D. | y=-x2+2x-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com