
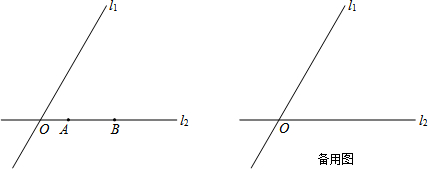
分析 (1)如图1,根据线段AB在平移的过程中长度不变,∠APB=30°为定值的特点,联想圆周角定理及其推论,构造以AB的长为半径的圆,即可解决问题.
(2)如图2、图3,当圆C与直线l1相切时,符合条件的点只有一个;作辅助线,运用切线的性质和三角函数的定义,分别求出OA的长,即可解决问题.
(3)如图4或图5,在⊙C运动的过程中,符合条件的点P有三个,分别运用切线的性质、矩形的性质、三角函数的定义求出OA的长度,即可解决问题.
解答 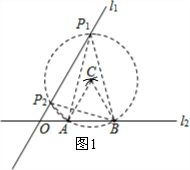 解:(1)如图1,以AB为边在x轴上方作等边三角形ABC,
解:(1)如图1,以AB为边在x轴上方作等边三角形ABC,
以C为圆心,AB长为半径作圆,与直线l1有两个交点P1、P2,
则P1、P2是符合条件的点.
(2)当点A在点O的右侧,OA=$\frac{4}{3}$$\sqrt{3}$时,或当点A在点O的左侧,OA=$\frac{4}{3}$$\sqrt{3}$+2时,符合条件的点P有且只有一个.理由如下:
如图2,当直线l1与⊙C相切于点P,且A在O的右侧时,则∠APB=30°,
连接CP,过A作AD⊥l1于D, 则AD=CP=2,
则AD=CP=2,
∴OA=$\frac{AD}{sin60°}$=$\frac{4}{3}$$\sqrt{3}$.
如图3,当直线l1与⊙C相切于点P,且A在O的左侧时,
则∠APB=30°;
连接CP,过B作BE⊥l1于E,
则BE=CP=2,
∴OB=$\frac{BE}{sin60°}$=$\frac{4}{3}$$\sqrt{3}$,
∴OA=$\frac{4}{3}$$\sqrt{3}$+2.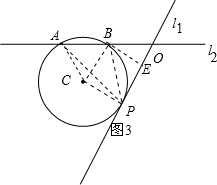
(3)存在:理由如下:
当A在O的右侧,OA=$\frac{4}{3}$$\sqrt{3}$-2,或A在O的左侧,OA=$\frac{4}{3}$$\sqrt{3}$时,
符合条件的点P有三个;理由如下:
如图4,当直线l1与⊙C1相交于点P1、P2,与⊙C2相切于点P3时,连接
C2P3,过O作OF⊥BC2于F,则OF=C2P3=2,
∴OB=$\frac{OF}{sin60°}$=$\frac{4}{3}$$\sqrt{3}$,
∴OA=$\frac{4}{3}$$\sqrt{3}$-2.
如图5,当直线l1与⊙C1相切于点P1,与⊙C2相交于点P2、P3时,连接
C1P1,过A作AG⊥l1于G,则AG=C1P1=2,
∴OA=$\frac{AG}{sin60°}$=$\frac{4}{3}$$\sqrt{3}$.
点评 该题以圆为载体,以平移变换为方法,以考查直线与圆的位置关系及其应用为核心构造而成;解题的方法是抓住图形在运动过程中的不变元素,动中求静,以静制动;解题的关键是借助辅助圆,灵活运用圆的切线的性质来分析、判断、推理或解答.


科目:初中数学 来源: 题型:解答题
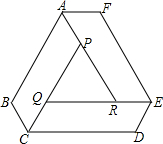 如图,工人师傅要做一张由3块完全相同的平行四边形木板和1块三角板木板拼成的六边形桌面ABCDEF,量得AB=90cm,BC=30cm
如图,工人师傅要做一张由3块完全相同的平行四边形木板和1块三角板木板拼成的六边形桌面ABCDEF,量得AB=90cm,BC=30cm查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知矩形ABCD的对角线相交于O,OF⊥AD,OF=2cm,AE⊥BD,且BE=OE
已知矩形ABCD的对角线相交于O,OF⊥AD,OF=2cm,AE⊥BD,且BE=OE查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com