练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    当m为何值时，4a2m-1•b+a2b-5是四次多项式？
    分析：根据多项式次数的定义求解．多项式的次数是多项式中最高次项的次数，即可得到关于m的方程，从而求解．
    解答：解：根据题意得：2m-1+1=4，
    解得：m=2，
    即当m=2时，4a2m-1•b+a2b-5是四次多项式．
    点评：此题考查的是多项式的定义，多项式中每个单项式叫做多项式的项，这些单项式中的最高次数，就是这个多项式的次数．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2013届江苏省张家港市塘桥初级中学初三第一学期调研试卷数学试卷（带解析） 题型：解答题

    已知关于x的方程a2x2+（2a－1）x+1=0有两个实数根x1，x2．（1）当a为何值时，x1≠x2；（2）是否存在实数a，使方程的两个实数根互为相反数？如果存在，求出a的值；如果不存在，说明理由．
    解：（1）根据题意，得△=（2a－1）2－4a2>0，解得a<．
    ∴当a<时，方程有两个不相等的实数根．
    （2）存在，如果方程的两个实数根x1，x2互为相反数，则x1+x2=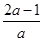－=0①，
    解得a=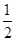，经检验，a=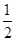是方程①的根．
    ∴当a=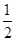时，方程的两个实数根x1与x2互为相反数．
    上述解答过程是否有错误？如果有，请指出错误之处，并解答．

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年江苏省张家港市初三第一学期调研试卷数学试卷（解析版） 题型：解答题

    已知关于x的方程a2x2+（2a－1）x+1=0有两个实数根x1，x2．（1）当a为何值时，x1≠x2；（2）是否存在实数a，使方程的两个实数根互为相反数？如果存在，求出a的值；如果不存在，说明理由．

    解：（1）根据题意，得△=（2a－1）2－4a2>0，解得a<．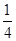

    ∴当a<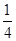时，方程有两个不相等的实数根．

    （2）存在，如果方程的两个实数根x1，x2互为相反数，则x1+x2=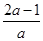－=0①，

    解得a=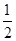，经检验，a=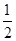是方程①的根．

    ∴当a=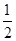时，方程的两个实数根x1与x2互为相反数．

    上述解答过程是否有错误？如果有，请指出错误之处，并解答．

     

    查看答案和解析>>

    同步练习册答案