
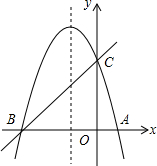
 如图,已知抛物线y=-x2+bx+c的对称轴为直线x=-1,与y轴交于点C(0,3),与x轴交于点A和点B.
如图,已知抛物线y=-x2+bx+c的对称轴为直线x=-1,与y轴交于点C(0,3),与x轴交于点A和点B.分析 (1)依据抛物线的对称轴公式可得到-$\frac{b}{2a}$=-1,然后在将点C的坐标代入可得到关于b、c的方程组,然后解得b、c的值即可;
(2)由轴对称的性质和两点之间线段最短的性质可知当点M在CB上时,AM+MC的值最小,然后求得BC的解析式,再把x=-1代入直线BC的解析式求得对应的y值即可;
(3)设P(-1,t),依据两点间的距离公式得到CB2=18,PB2=t2+4,PC2=t2-6t+10,然后分为BC2+PB2=PC2、BC2+PC2=PB2、PC2+PB2=BC2三种情况列方程求解即可.
解答 解:(1)根据题意得:-$\frac{b}{2×(-1)}$=-1,c=3,解得:b=-2,c=3,
∴抛物线的解析式为:y=-x2-2x+3,
当y=0时,即0=-x2-2x+3,
解得:x1=-3,x2=1,
∴A(1,0),B(-3,0);
(2)设直线BC与对称轴x=-1的交点为M,则此时AM+MC的值最小.
∵点A与点B关于x=-1对称,A(1,0),
∴C(-3,0).
设BC的解析式为y=mx+n,将点B和点C的坐标代入得:$\left\{\begin{array}{l}{n=3}\\{-3m+n=0}\end{array}\right.$,解得:m=1,n=3.
∴直线BC的解析式为y=x+3.
将x=-1代入y=x+3得:y=2,
∴M(-1,2).
∴当点M的坐标为(-1,2)时,点M到点A和点C的距离之和最小;
(3)设P(-1,t).
∵P(-1,t),B(-3,0),C(0,3),
∴CB2=18,PB2=(-1+3)2+t2=t2+4,PC2=(-1)2+(t-3)2=t2-6t+10.
①当点B为直角顶点时,则BC2+PB2=PC2,即18+t2+4=t2-6t+10,解得t=-2,
∴P(-1,-2).
②当点C为直角顶点时,BC2+PC2=PB2,即18+t2-6t+10=t2+4,解得t=4,
∴P(-1,4).
③当点P为直角顶点时,PC2+PB2=BC2,即t2+4+t2-6t+10=18,解得:t=$\frac{3+\sqrt{17}}{2}$或t=$\frac{3-\sqrt{17}}{2}$,
∴P(-1,$\frac{3+\sqrt{17}}{2}$)或(-1,$\frac{3-\sqrt{17}}{2}$).
综上所述,点P的坐标为P(-1,-2)或(-1,4)或(-1,$\frac{3+\sqrt{17}}{2}$)或(-1,$\frac{3-\sqrt{17}}{2}$).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的关系式,轴对称图形的性质、勾股定理的逆定理的应用,依据勾股定理的逆定理列出关于t的方程是解题的关键.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
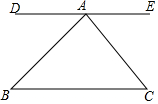 如图,直线DE经过点A,DE∥BC,∠B=45°,∠C=50°,
如图,直线DE经过点A,DE∥BC,∠B=45°,∠C=50°,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,$\widehat{AC}$恰好经过点O,则$\widehat{BC}$与$\widehat{AC}$的关系是( )
如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,$\widehat{AC}$恰好经过点O,则$\widehat{BC}$与$\widehat{AC}$的关系是( )| A. | $\widehat{BC}$=$\frac{1}{2}$$\widehat{AC}$ | B. | $\widehat{BC}$=$\frac{1}{3}$$\widehat{AC}$ | C. | $\widehat{BC}$=$\widehat{AC}$ | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com