
【题目】有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
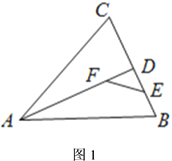
(1)如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点.求证:四边形
上的点.求证:四边形![]() 是邻余四边形;
是邻余四边形;
(2)如图2,已知![]() ,点
,点![]() 在
在![]() 的垂直平分线上,
的垂直平分线上,![]() 在边
在边![]() 上,
上,![]() 是
是![]() 内一点, 连接
内一点, 连接![]() ,
,![]() ,
,![]() ,
,![]() ,若四边形
,若四边形![]() 是邻余四边形,
是邻余四边形,![]() 是邻余线.
是邻余线.
①![]() 与
与![]() 有什么位置关系?说明理由.
有什么位置关系?说明理由.
②判断![]() 形状,说明理由.
形状,说明理由.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(3)班“2017年新年联欢会”中,有一个摸奖游戏,规则如下:有4张纸牌,背面都是喜羊羊头像,正面有2张笑脸、2张哭脸.现将4张纸牌洗匀后背面朝上摆放到桌上,然后让同学去翻纸牌.
(1)现小芳有一次翻牌机会,若正面是笑脸的就获奖,正面是哭脸的不获奖.她从中随机翻开一张纸牌,求小芳获奖的概率.
(2)如果小芳、小明都有翻两张牌的机会.小芳先翻一张,放回后再翻一张;小明同时翻开两张纸牌.他们翻开的两张纸牌中只要出现一张笑脸就获奖.他们获奖的机会相等吗?通过树状图分析说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
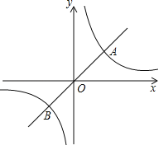
【题目】如图,定义:若双曲线![]() (k>0)与它的其中一条对称轴y=x相交于A、B两点,则线段AB的长度为双曲线
(k>0)与它的其中一条对称轴y=x相交于A、B两点,则线段AB的长度为双曲线![]() (k>0)的对径.
(k>0)的对径.
(1)求双曲线![]() 的对径.
的对径.
(2)若双曲线![]() (k>0)的对径是
(k>0)的对径是![]() ,求k的值.
,求k的值.
(3)仿照上述定义,定义双曲线![]() (k<0)的对径.
(k<0)的对径.
查看答案和解析>>
科目:初中数学 来源: 题型:
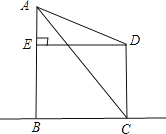
【题目】两建筑物AB和CD的水平距离为30米,如图所示,从A点测得太阳落山时,太阳光线AC照射到AB后的影子恰好在CD的墙角时的角度∠ACB=60°,又过一会儿,当AB的影子正好到达CD的楼顶D时的角度∠ADE=30°,DE⊥AB于E,则建筑物CD的高是多少米?(![]() ≈1.732,结果保留两位有效数字)
≈1.732,结果保留两位有效数字)
查看答案和解析>>
科目:初中数学 来源: 题型:
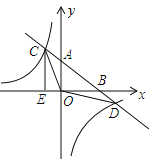
【题目】如图,一次函数y=ax+b的图象与反比例函数![]() 的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=
的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求一次函数的解析式和反比例函数的解析式;
(2)求△OCD的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有两个圆,![]() 的半径等于篮球的半径,
的半径等于篮球的半径,![]() 的半径等于一个乒乓球的半径,现将两个圆的周长都增加
的半径等于一个乒乓球的半径,现将两个圆的周长都增加![]() 米,则面积增加较多的圆是( )
米,则面积增加较多的圆是( )
A. ![]() B.
B. ![]()
C. 两圆增加的面积是相同的 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 经过
经过![]() ,
,![]() ,顶点为
,顶点为![]() .
.
![]() 求该抛物线的表达方式及点
求该抛物线的表达方式及点![]() 的坐标;
的坐标;
![]() 将
将![]() 中求得的抛物线沿
中求得的抛物线沿![]() 轴向上平移
轴向上平移![]() 个单位,所得新抛物线与
个单位,所得新抛物线与![]() 轴的交点记为点
轴的交点记为点![]() .当
.当![]() 时等腰三角形时,求点
时等腰三角形时,求点![]() 的坐标;
的坐标;
![]() 若点
若点![]() 在
在![]() 中求得的抛物线的对称轴上,联结
中求得的抛物线的对称轴上,联结![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针转
逆时针转![]() 得到线段
得到线段![]() ,若点
,若点![]() 恰好落在
恰好落在![]() 中求得的抛物线上,求点
中求得的抛物线上,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com