
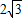 km处.
km处.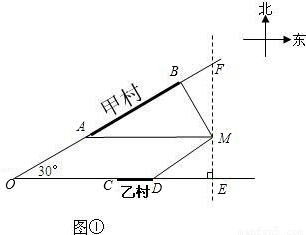

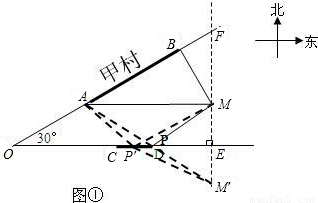 解:方案一:
解:方案一: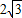 (km);(3分)
(km);(3分) AM,
AM,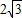 ×
×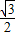 =3,
=3, DM=
DM= ×
×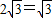 ,
,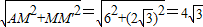 ;(7分)
;(7分)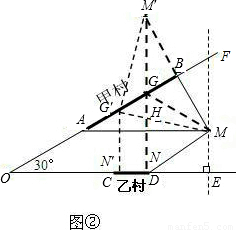
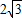 ,∴M'D=
,∴M'D=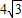 (10分)
(10分)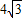 ,(11分)
,(11分)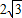 <
<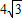 ,
,

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源:2008年全国中考数学试题汇编《尺规作图》(01)(解析版) 题型:解答题
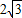 km处.
km处.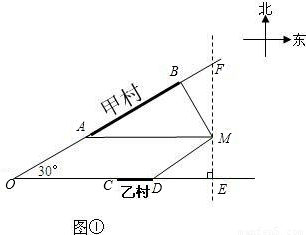
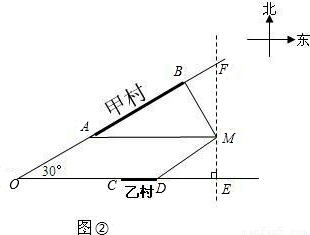
查看答案和解析>>
科目:初中数学 来源:2010年中考数学考前知识点回归+巩固 专题24 抽样与数据的分析(解析版) 题型:解答题
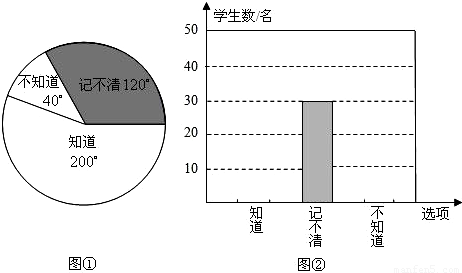
查看答案和解析>>
科目:初中数学 来源:2010年中考数学考前知识点回归+巩固 专题20 图形的相似(解析版) 题型:解答题
 km处.
km处.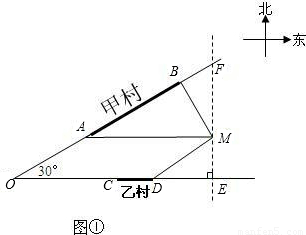
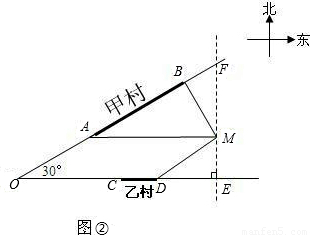
查看答案和解析>>
科目:初中数学 来源:2010年江苏省泰州市九年级下学期六校联考数学试卷(解析版) 题型:解答题
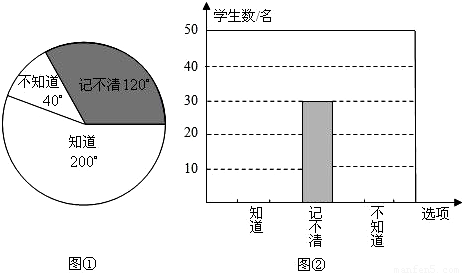
查看答案和解析>>
科目:初中数学 来源:2010年江苏省南通市初三中考数学模拟测试卷(解析版) 题型:解答题
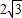 km处.
km处.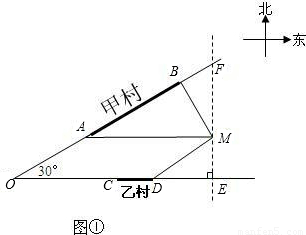
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com