
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对旅客上飞机前的安检 | |
| B. | 了解全班同学每周体育锻炼的时间 | |
| C. | 调查奥运会金牌获得者的兴奋剂使用情况 | |
| D. | 调查我国居民对汽车废气污染环境的看法 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
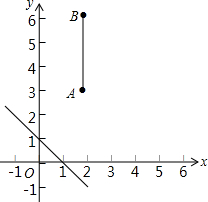 如果,在平面直角坐标系中,已知点A(2,3)、B(2,6),连接AB,如果点P在直线y=-x+1上,且点P到直线的距离小于1,那么点P是线段AB的“环绕点”,若点Q(m,n)是线段AB的“环绕点”,求n的取值范围.
如果,在平面直角坐标系中,已知点A(2,3)、B(2,6),连接AB,如果点P在直线y=-x+1上,且点P到直线的距离小于1,那么点P是线段AB的“环绕点”,若点Q(m,n)是线段AB的“环绕点”,求n的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x-2=x | B. | x2-2x=2x | C. | x-2=2x | D. | x=2x-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 -$\frac{{x}^{2}-1}{{x}^{2}-2x+1}$)÷$\frac{x}{x+1}$=$\frac{x+1}{x-1}$
-$\frac{{x}^{2}-1}{{x}^{2}-2x+1}$)÷$\frac{x}{x+1}$=$\frac{x+1}{x-1}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
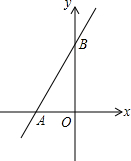 如图,平面直角坐标系中,点O为坐标原点,一次函数的图象过点(-1,4)与点(3,12).
如图,平面直角坐标系中,点O为坐标原点,一次函数的图象过点(-1,4)与点(3,12).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
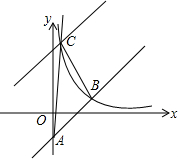 如图,已知直线y=x+a与y轴相交于点A,与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点B(-a+1,a+4).
如图,已知直线y=x+a与y轴相交于点A,与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点B(-a+1,a+4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com