
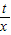 ŌŚµŚŅ»ĻóĻŽĻą½»ÓŚµćC£»ŅŌACĪŖŠ±±ß”¢”ĻCAOĪŖÄŚ½ĒµÄÖ±½ĒČż½ĒŠĪ£¬ÓėŅŌCOĪŖ¶Ō½ĒĻß”¢Ņ»±ßŌŚxÖįÉĻµÄ¾ŲŠĪĆ껿ĻąµČ£»µćC£¬PŌŚŅŌBĪŖ¶„µćµÄÅ×ĪļĻßy=mx2+nx+kÉĻ£»Ö±Ļßy=hx+d”¢Ė«ĒśĻßy=
ŌŚµŚŅ»ĻóĻŽĻą½»ÓŚµćC£»ŅŌACĪŖŠ±±ß”¢”ĻCAOĪŖÄŚ½ĒµÄÖ±½ĒČż½ĒŠĪ£¬ÓėŅŌCOĪŖ¶Ō½ĒĻß”¢Ņ»±ßŌŚxÖįÉĻµÄ¾ŲŠĪĆ껿ĻąµČ£»µćC£¬PŌŚŅŌBĪŖ¶„µćµÄÅ×ĪļĻßy=mx2+nx+kÉĻ£»Ö±Ļßy=hx+d”¢Ė«ĒśĻßy=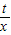 ŗĶÅ×ĪļĻßy=ax2+bx+cĶ¬Ź±¾¹żĮ½øö²»Ķ¬µÄµćC£¬D£®
ŗĶÅ×ĪļĻßy=ax2+bx+cĶ¬Ź±¾¹żĮ½øö²»Ķ¬µÄµćC£¬D£®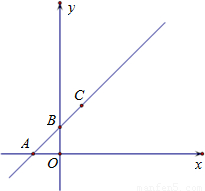
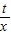 ¾¹żµćC£Øx1£¬y1£©£¬x1y1=t£®
¾¹żµćC£Øx1£¬y1£©£¬x1y1=t£® ×y1×£Ø1+x1£©£»
×y1×£Ø1+x1£©£» ×y1×£Ø1+x1£©=x1y1£¬
×y1×£Ø1+x1£©=x1y1£¬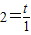 £¬
£¬ £¬
£¬ £¬
£¬
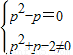
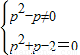 £¬
£¬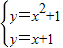 £Ø7·Ö£©
£Ø7·Ö£©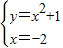 £Ø10·Ö£©
£Ø10·Ö£© ½āµĆ½»µćĪŖC£Ø1£¬2£©£® £Ø12·Ö£©
½āµĆ½»µćĪŖC£Ø1£¬2£©£® £Ø12·Ö£©


| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| t |
| x |
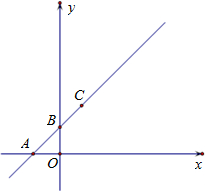 hx+d”¢Ė«ĒśĻßy=
hx+d”¢Ė«ĒśĻßy=| t |
| x |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
ČēĶ¼£¬Ö±Ļßy=hx+dÓėxÖįŗĶyÖį·Ö±šĻą½»ÓŚµćA(-1,0),B(0,1),ÓėĖ«ĒśĻßy=ŌŚµŚŅ»ĻóĻŽĻą½»ÓŚµćC£»ŅŌACĪŖŠ±±ß”¢
ĪŖÄŚ½ĒµÄÖ±½ĒČż½ĒŠĪ£¬ÓėŅŌCOĪŖ¶Ō½ĒĻß”¢Ņ»±ßŌŚxÖįÉĻµÄ¾ŲŠĪĆ껿ĻąµČ£»µćC,PŌŚŅŌBĪŖ¶„µćµÄÅ×ĪļĻßy=
ÉĻ£»Ö±Ļßy=hx+d”¢Ė«ĒśĻßy=
ŗĶÅ×ĪļĻß
Ķ¬Ź±¾¹żĮ½øö²»Ķ¬µÄµćC£¬D
£Ø1£©Č·¶ØtµÄÖµ
£Ø2£©Č·¶Øm , n , kµÄÖµ
£Ø3£©ČōĪŽĀŪa , b , cŗĪÖµ£¬Å×ĪļĻ߶¼²»¾µćP£¬ĒėČ·¶ØP×ų±ź£Ø12·Ö£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2010ğȫ¹śÖŠæ¼ŹżŃ§ŹŌĢā»ć±ą”¶Ņ»“ĪŗÆŹż”·£Ø07£©£Ø½āĪö°ę£© ĢāŠĶ£ŗ½ā“šĢā
 ŌŚµŚŅ»ĻóĻŽĻą½»ÓŚµćC£»ŅŌACĪŖŠ±±ß”¢”ĻCAOĪŖÄŚ½ĒµÄÖ±½ĒČż½ĒŠĪ£¬ÓėŅŌCOĪŖ¶Ō½ĒĻß”¢Ņ»±ßŌŚxÖįÉĻµÄ¾ŲŠĪĆ껿ĻąµČ£»µćC£¬PŌŚŅŌBĪŖ¶„µćµÄÅ×ĪļĻßy=mx2+nx+kÉĻ£»Ö±Ļßy=hx+d”¢Ė«ĒśĻßy=
ŌŚµŚŅ»ĻóĻŽĻą½»ÓŚµćC£»ŅŌACĪŖŠ±±ß”¢”ĻCAOĪŖÄŚ½ĒµÄÖ±½ĒČż½ĒŠĪ£¬ÓėŅŌCOĪŖ¶Ō½ĒĻß”¢Ņ»±ßŌŚxÖįÉĻµÄ¾ŲŠĪĆ껿ĻąµČ£»µćC£¬PŌŚŅŌBĪŖ¶„µćµÄÅ×ĪļĻßy=mx2+nx+kÉĻ£»Ö±Ļßy=hx+d”¢Ė«ĒśĻßy= ŗĶÅ×ĪļĻßy=ax2+bx+cĶ¬Ź±¾¹żĮ½øö²»Ķ¬µÄµćC£¬D£®
ŗĶÅ×ĪļĻßy=ax2+bx+cĶ¬Ź±¾¹żĮ½øö²»Ķ¬µÄµćC£¬D£®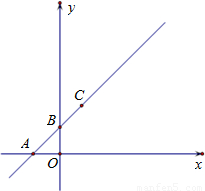
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2010Äźøß¼¶ÖŠµČѧŠ£ÕŠÉśČ«¹śĶ³Ņ»æ¼ŹŌŹżŃ§¾ķ£Ø¹ćĪ÷ÄĻÄž£© ĢāŠĶ£ŗ½ā“šĢā
ČēĶ¼£¬Ö±Ļßy=hx+dÓėxÖįŗĶyÖį·Ö±šĻą½»ÓŚµćA(-1,0),B(0,1),ÓėĖ«ĒśĻßy= ŌŚµŚŅ»ĻóĻŽĻą½»ÓŚµćC£»ŅŌACĪŖŠ±±ß”¢
ŌŚµŚŅ»ĻóĻŽĻą½»ÓŚµćC£»ŅŌACĪŖŠ±±ß”¢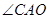 ĪŖÄŚ½ĒµÄÖ±½ĒČż½ĒŠĪ£¬ÓėŅŌCOĪŖ¶Ō½ĒĻß”¢Ņ»±ßŌŚxÖįÉĻµÄ¾ŲŠĪĆ껿ĻąµČ£»µćC,PŌŚŅŌBĪŖ¶„µćµÄÅ×ĪļĻßy=
ĪŖÄŚ½ĒµÄÖ±½ĒČż½ĒŠĪ£¬ÓėŅŌCOĪŖ¶Ō½ĒĻß”¢Ņ»±ßŌŚxÖįÉĻµÄ¾ŲŠĪĆ껿ĻąµČ£»µćC,PŌŚŅŌBĪŖ¶„µćµÄÅ×ĪļĻßy= ÉĻ£»Ö±Ļßy=hx+d”¢Ė«ĒśĻßy=
ÉĻ£»Ö±Ļßy=hx+d”¢Ė«ĒśĻßy= ŗĶÅ×ĪļĻß
ŗĶÅ×ĪļĻß Ķ¬Ź±¾¹żĮ½øö²»Ķ¬µÄµćC£¬D
Ķ¬Ź±¾¹żĮ½øö²»Ķ¬µÄµćC£¬D

£Ø1£©Č·¶ØtµÄÖµ
£Ø2£©Č·¶Øm , n , kµÄÖµ
£Ø3£©ČōĪŽĀŪa , b , cŗĪÖµ£¬Å×ĪļĻß ¶¼²»¾µćP£¬ĒėČ·¶ØP×ų±ź£Ø12·Ö£©
¶¼²»¾µćP£¬ĒėČ·¶ØP×ų±ź£Ø12·Ö£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2010ÄźĖÄ“ØćņÖŻĢģĮ¢Ń§Š£³õŅ»µŚŅ»Ń§ĘŚĘŚÖŠŹżŃ§¾ķ ĢāŠĶ£ŗ½ā“šĢā
ČēĶ¼£¬Ö±Ļßy=hx+dÓėxÖįŗĶyÖį·Ö±šĻą½»ÓŚµćA(-1,0),B(0,1),ÓėĖ«ĒśĻßy= ŌŚµŚŅ»ĻóĻŽĻą½»ÓŚµćC£»ŅŌACĪŖŠ±±ß”¢
ŌŚµŚŅ»ĻóĻŽĻą½»ÓŚµćC£»ŅŌACĪŖŠ±±ß”¢ ĪŖÄŚ½ĒµÄÖ±½ĒČż½ĒŠĪ£¬ÓėŅŌCOĪŖ¶Ō½ĒĻß”¢Ņ»±ßŌŚxÖįÉĻµÄ¾ŲŠĪĆ껿ĻąµČ£»µćC,PŌŚŅŌBĪŖ¶„µćµÄÅ×ĪļĻßy=
ĪŖÄŚ½ĒµÄÖ±½ĒČż½ĒŠĪ£¬ÓėŅŌCOĪŖ¶Ō½ĒĻß”¢Ņ»±ßŌŚxÖįÉĻµÄ¾ŲŠĪĆ껿ĻąµČ£»µćC,PŌŚŅŌBĪŖ¶„µćµÄÅ×ĪļĻßy= ÉĻ£»Ö±Ļßy=hx+d”¢Ė«ĒśĻßy=
ÉĻ£»Ö±Ļßy=hx+d”¢Ė«ĒśĻßy= ŗĶÅ×ĪļĻß
ŗĶÅ×ĪļĻß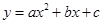 Ķ¬Ź±¾¹żĮ½øö²»Ķ¬µÄµćC£¬D
Ķ¬Ź±¾¹żĮ½øö²»Ķ¬µÄµćC£¬D

£Ø1£©Č·¶ØtµÄÖµ
£Ø2£©Č·¶Øm , n , kµÄÖµ
£Ø3£©ČōĪŽĀŪa , b , cŗĪÖµ£¬Å×ĪļĻß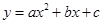 ¶¼²»¾µćP£¬ĒėČ·¶ØP×ų±ź£Ø12·Ö£©
¶¼²»¾µćP£¬ĒėČ·¶ØP×ų±ź£Ø12·Ö£©
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com