练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．如图，菱形ABCD中，已知∠D=110°，则∠BAC的度数为（　　）
    A．30°B．35°C．40°D．45°

    分析 先根据菱形的对边平行和直线平行的性质得到∠BAD=70°，然后根据菱形的每一条对角线平分一组对角求解．

    解答 解：∵四边形ABCD为菱形，
    ∴AD∥AB，
    ∴∠BAD=180°-∠D=180°-110°=70°，
    ∵四边形ABCD为菱形，
    ∴AC平分∠BAD，
    ∴∠BAC=$\frac{1}{2}$∠BAD=35°．
    故选B．

    点评 本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．在矩形ABCD中，已知AB=2，BC=4，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，求CE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知∠ABC=∠DEF=∠ACB，△DBE与△ECF相似吗？（证一证）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．一组数据5，x，8，2，3的平均数是4，则这组数据的中位数是3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

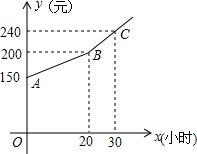    10．为了鼓励小强做家务，小强每月的生活总费用都是由基本生活费和上月根据他的家务劳动时间所获得的奖励两部分组成．若设小强每月的家务劳动时间为x小时．下月他可获得的生活总费用为y元，則y（元）和x（小时）之间的函数图象如图所示．
    （1）根据图象回答问题：小强每月的基本生活费是150元；若小强4月份做家务10小时，則他5月份能获得175元生活总费用；
    （2）根据图象求出AB段的函数表达式；
    （3）若小強希望5月份有250元的生活总费用，则小强4月份需做家务多少小时？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知A、B两地的路程为240千米，某经销商每天都要用汽车或火车将x吨保鲜品一次性由A地运往B地，受各种因素限制，下一周只能采用汽车或火车中的一种进行运输，且须提前预订，现有货运收费项目及收费村准表、行驶路程s（千米）与行驶时间t（时）的函数图象（如图1）、上周货运量折线统计图（如图2）等信息如下：

    货运收费项目及收费标准表
    运输工具运输费单价：元/（吨•千米）冷藏费单价：元/（吨•时）固定费用：元/次
    汽车25200
    火车1.652280
    （1）汽车的速度为60千米/时，火车的速度为100千米/时；
    （2）设每于用汽车和火车运输的总费用分别为y汽（元）和y火（元），分别求y汽、y火与x的函数关系式（不必写出x的取值范围），及x为何值时y汽＞y火（总费用=运输费+冷藏费+固定费用）；
    （3）根据上周货运量的折线统计图，请你从平均数和折线图走势两个角度分析，建议该经销商应提前为下周预定哪种运输工具，才能使每天的运输总费用较省？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

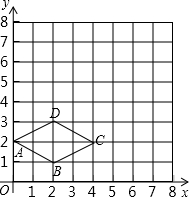    7．如图，在平面直角坐标系中，菱形ABCD各顶点均在格点上．
    （1）写出菱形ABCD各顶点的坐标；
    （2）将菱形ABCD各顶点的横纵坐标都乘2，对应的点依次记作A′，B′，C′，D′，请在图中画出四边形A′B′C′D′．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

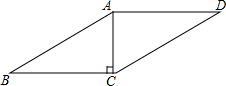    4．如图，在?ABCD中，过A点作高，垂足刚好为点C，AB=4，AC=2，则?ABCD的周长是（　　）
    A．8+4$\sqrt{3}$B．4+2$\sqrt{3}$C．8D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．先化简，再求值：[（2x-y）2-（y+2x）（y-2x）]÷（-2x），其中x=-$\frac{1}{2}$，y=3．

    查看答案和解析>>

    同步练习册答案