
 如图,反比例函数y=$\frac{k}{x}$的图象经过点A(-1,4),直线y=-x+b(b≠0)与双曲线y=$\frac{k}{x}$在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.
如图,反比例函数y=$\frac{k}{x}$的图象经过点A(-1,4),直线y=-x+b(b≠0)与双曲线y=$\frac{k}{x}$在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.分析 (1)根据反比例函数的图象上点的坐标特征易得k=-4;
(2)当b=-2时,直线解析式为y=-x-2,则利用坐标轴上点的坐标特征可求出C(-2,0),D(0,-2),然后根据三角形面积公式求解;
(3)先表示出C(b,0),根据三角形面积公式,由于S△ODQ=S△OCD,所以点Q和点C到OD的距离相等,则Q的横坐标为(-b,0),利用直线解析式可得到Q(-b,2b),再根据反比例函数的图象上点的坐标特征得到-b•2b=-4,然后解方程即可得到满足条件的b的值.
解答 解:(1)∵反比例函数y=$\frac{k}{x}$的图象经过点A(-1,4),
∴k=-1×4=-4;
(2)当b=-2时,直线解析式为y=-x-2,
∵y=0时,-x-2=0,解得x=-2,
∴C(-2,0),
∵当x=0时,y=-x-2=-2,
∴D(0,-2),
∴S△OCD=$\frac{1}{2}$×2×2=2;
(3)存在.
当y=0时,-x+b=0,解得x=b,则C(b,0),
∵S△ODQ=S△OCD,
∴点Q和点C到OD的距离相等,
而Q点在第四象限,
∴Q的横坐标为-b,
当x=-b时,y=-x+b=2b,则Q(-b,2b),
∵点Q在反比例函数y=-$\frac{4}{x}$的图象上,
∴-b•2b=-4,解得b=-$\sqrt{2}$或b=$\sqrt{2}$(舍去),
∴b的值为-$\sqrt{2}$.
点评 本题考查了反比例函数与一次函数的交点:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了反比例函数图象上点的坐标特征和三角形面积公式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
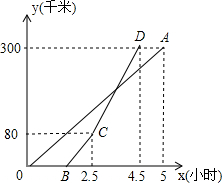 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA和折线BCD分别表示货车和轿车离甲地距离y(千米)与车行驶时间x(小时)之间的函数关系.请根据图象解答下列问题:
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA和折线BCD分别表示货车和轿车离甲地距离y(千米)与车行驶时间x(小时)之间的函数关系.请根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≤2 | B. | 1≤a≤2 | C. | 1≤a<2 | D. | a≥1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
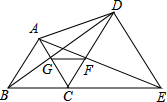 如图,已知B、C、E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F,求证:
如图,已知B、C、E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F,求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,0) | B. | (0,2) | C. | (2,-4) | D. | (-4,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
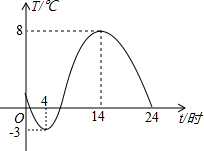 如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )| A. | 凌晨4时气温最低为-3℃ | |
| B. | 14时气温最高为8℃ | |
| C. | 从0时至14时,气温随时间增长而上升 | |
| D. | 从14时至24时,气温随时间增长而下降 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
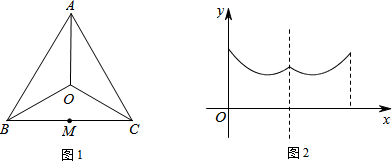
| A. | A→O→B | B. | B→A→C | C. | B→O→C | D. | C→B→O |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com