

���� ��1������DM���ӳ�����BN��AB����DM���ӳ��߽���N������CN����֤����EMD�ա�BMN���õ�BN=DE=DA����֤����CAD�ա�CNB���õ�CD=CN��֤����DCM�ǵ���ֱ�������μ��ɣ�
��2��̽��һ���ӳ�DM��BC��N������ƽ���ߵ����ʺ��ж��Ƴ���DEM=��MBC������ASA�Ƴ���EMD�ա�BMN��֤��BN=AD��֤����CMDΪ����ֱ�������μ��ɣ�
̽��������BN��DE��DM���ӳ�����N������CN������ƽ���ߵ����������E=��NBM������ASA֤��DCA�ա�NCB���Ƴ���DCN�ǵ���ֱ�������Σ����ݵ���ֱ�������ε����ʼ����Ƴ���CMDΪ����ֱ�������Σ�
��� �⣺��1����ͼһ������DM���ӳ�����BN��AB����DM���ӳ��߽���N������CN��
�ߡ�EDA=��ABN=90�㣬
��DE��BN��
���DEM=��MBN��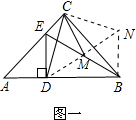
���ڡ�EMD�͡�BMN�У�
$\left\{\begin{array}{l}{��DEM=��NBM}\\{EM=BM}\\{��EMD=��NMB}\end{array}\right.$��
���EMD�ա�BMN��ASA����
��BN=DE=DA��MN=MD��
�ڡ�CAD�͡�CNB�У�
$\left\{\begin{array}{l}{AC=BC}\\{��A=��CBN=45��}\\{BN=DA}\end{array}\right.$��
���CAD�ա�CNB��
��CD=CN��
���DCN�ǵ���ֱ�������Σ���CM�ǵױߵ����ߣ�
��CM��DN��
���DCM�ǵ���ֱ�������Σ�
��DM=CM��
��2��̽��һ��
���ɣ���ͼ��������DM���ӳ�DM��BC��N��
�ߡ�EDA=��ACB=90�㣬
��DE��BC��
���DEM=��MBC��
���ڡ�EMD�͡�BMN�У�
$\left\{\begin{array}{l}{��DEM=��NBM}\\{EM=BM}\\{��EMD=��NMB}\end{array}\right.$��
���EMD�ա�BMN��ASA����
��BN=DE=DA��MN=MD
��AC=BC��
��CD=CN��
���DCN�ǵ���ֱ�������Σ���CM�ǵױߵ����ߣ�
��CM��DM����DCM=$\frac{1}{2}$��DCN=45��=��BCM��
���CMDΪ����ֱ�������Σ�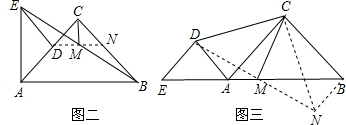
��DM=CM��
̽������
���ɣ���ͼ��������DM������B��BN��DE��DM���ӳ�����N������CN��
���E=��MBN=45�㣮
�ߵ�M��BE���е㣬
��EM=BM��
���ڡ�EMD�͡�BMN�У�
$\left\{\begin{array}{l}{��E=��MBN}\\{EM=BM}\\{��DME=��NMB}\end{array}\right.$
���EMD�ա�BMN��ASA����
��BN=DE=DA��MN=MD��
�ߡ�DAE=��BAC=��ABC=45�㣬
���DAC=��NBC=90��
���ڡ�DCA�͡�NCB��
$\left\{\begin{array}{l}{DA=BN}\\{��DAC=��NBC}\\{CA=BC}\end{array}\right.$��
���DCA�ա�NCB��SAS����
���DCA=��NCB��DC=CN��
���DCN=��ACB=90�㣬
���DCN�ǵ���ֱ�������Σ���CM�ǵױߵ����ߣ�
��CM��DM����DCM=$\frac{1}{2}$��DCN=45��=��CDM��
���CMDΪ����ֱ�������Σ�
��DM=CM
���� �����ۺϿ����˵���ֱ�������Σ����������ε����ʺ��ж���ƽ���ߵ����ʺ��ж���ȫ�������ε����ʺ��ж��������ۺ��ԱȽ�ǿ��������ѧ����������ͽ����������������˼������ã����ͽϺã��ѶȽϴ�


 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
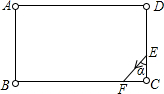 ��ͼ������̨����ABCD������A��B��C��D��������֪DE=4��CE=2��BC=6$\sqrt{3}$�����E���������DC�н�Ϊ��������BC��AB��AD���η�����ص�E�㣬��tan����ȡֵ��Χ��������
��ͼ������̨����ABCD������A��B��C��D��������֪DE=4��CE=2��BC=6$\sqrt{3}$�����E���������DC�н�Ϊ��������BC��AB��AD���η�����ص�E�㣬��tan����ȡֵ��Χ��������| A�� | $\sqrt{3}$��tan����$\frac{3}{2}$$\sqrt{3}$ | B�� | $\frac{3\sqrt{3}}{4}$��tan����$\frac{3}{2}$$\sqrt{3}$ | C�� | tan��=$\sqrt{3}$ | D�� | $\frac{3\sqrt{3}}{4}$��tan����3$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
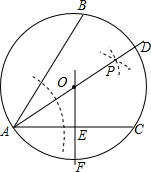 ��ͼ����A��B��C��һ����֪Բ�ϣ�ͨ��һ�������ij߹���ͼ����������AP����֪Բ�ڵ�D��ֱ��OF��ֱƽ��AC����AD�ڵ�O����AC�ڵ�E������֪Բ�ڵ�F��
��ͼ����A��B��C��һ����֪Բ�ϣ�ͨ��һ�������ij߹���ͼ����������AP����֪Բ�ڵ�D��ֱ��OF��ֱƽ��AC����AD�ڵ�O����AC�ڵ�E������֪Բ�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����y=x2+$\frac{4}{{x}^{2}}$��ͼ����ͼ��ʾ�����ڸú������н�����ȷ���Ǣ٢ڢۣ�����ţ���
����y=x2+$\frac{4}{{x}^{2}}$��ͼ����ͼ��ʾ�����ڸú������н�����ȷ���Ǣ٢ڢۣ�����ţ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
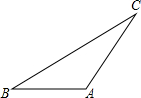 ����������䣬��������Ҫ���ͼ�Σ���Ҫ��д������
����������䣬��������Ҫ���ͼ�Σ���Ҫ��д�������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com