
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:解答题
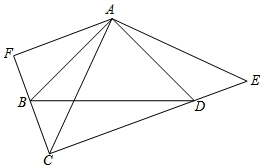 如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.
如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
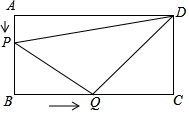
 如图,在四边形ABCD中,AD平行且等于BC,AB平行且等于DC,AD⊥AB,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点.
如图,在四边形ABCD中,AD平行且等于BC,AB平行且等于DC,AD⊥AB,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
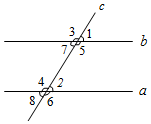 如图,直线a、b都与直线c相交,有下列条件:①∠1=∠2;②∠3+∠8=180°;③∠4=∠5;④∠6+∠7=180°.其中,能够判断a∥b的是( )
如图,直线a、b都与直线c相交,有下列条件:①∠1=∠2;②∠3+∠8=180°;③∠4=∠5;④∠6+∠7=180°.其中,能够判断a∥b的是( )| A. | ①② | B. | ②③④ | C. | ①③ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
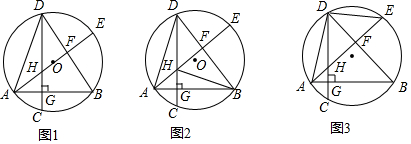
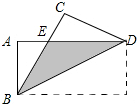 如图,把长方形ABCD沿对角线BD折叠,重合部分为△EBD.
如图,把长方形ABCD沿对角线BD折叠,重合部分为△EBD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com