练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，若以原点为位似中心，将五边形AEDCB放大，使放大后的五边形的边长是原五边形对应边长的3倍，请在下图网格中画出放大后的五边形。

    作图见解析.

    解析试题分析：连接OA，OB，OC，OD，OE，并延长到A′，B′，C′，D′，E′，使OA′，OB′，OC′，OD′，OE′是OA，OB，OC，OD，OE的3倍，顺次连接各点即可．
    试题解析：如图所示，

    五边形A'E'D'C'B'为所求五边形．
    考点: 作图-位似变换．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”．
    （1）请用直尺和圆规画一个“好玩三角形”；
    （2）如图1，在Rt△ABC中，∠C=90°，tanA= ，求证：△ABC是“好玩三角形”；
    （3）如图2，已知菱形ABCD的边长为a，∠ABC=2β，点P，Q从点A同时出发，以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动，记点P经过的路程为s．
    ①当β=45°时，若△APQ是“好玩三角形”，试求的值；
    ②当tanβ的取值在什么范围内，点P，Q在运动过程中，有且只有一个△APQ能成为“好玩三角形”．请直接写出tanβ的取值范围．
    （4）依据（3）的条件，提出一个关于“在点P，Q的运动过程中，tanβ的取值范围与△APQ是‘好玩三角形’的个数关系”的真命题（“好玩三角形”的个数限定不能为1）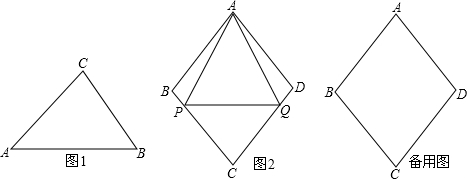

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在梯形中，∥，点是边的中点，连接交于，的延长线交的延长线于．

    （1）求证：；（2）若，，求线段的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在△中，，平分∠，∥．求证：．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图,网格图的每个小正方形边长均为1．△OAB的顶点均在格点上．已知△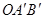与△OAB是以O为位似中心的位似图形,且位似比为1︰3．

    （1）请在第一象限内画出△;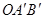
    （2）试求出△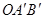的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    提出问题：如图①,在四边形ABCD中,点E、F是AD的n等分点中最中间2个,点G、H是BC的n等分点中最中间2个,（其中n为奇数）,连接EG、FH,那么S四边形EFHG与S四边形ABCD之间有什么关系呢？
                                             
    探究发现：为了解决这个问题,我们可以先从一些简单的、特殊的情形入手：
    (1)如图②：四边形ABCD中,点E、F是AD的3等分点,点G、H是BC的3等分点,连接EG、FH,那么S四边形EFHG与S四边形ABCD之间有什么关系呢？
    如图③,连接EH、BE、DH,

    因为△EGH与△EBH高相等,底的比是1:2,
    所以S△EGH=S△EBH
    因为△EFH与△DEH高相等,底的比是1:2,
    所以S△EFH=S△DEH
    所以S△EGH+S△EFH=S△EBH +S△DEH
    即S四边形EFHG=S四边形EBHD
    连接BD,
    因为△DBE与△ABD高相等,底的比是2：3,
    所以S△DBE=S△ABD
    因为△BDH与△BCD高相等,底的比是2：3,
    所以S△BDH=S△BCD
    所以S△DBE +S△BDH=S△ABD+S△BCD =(S△ABD+S△BCD)
    =S四边形ABCD
    即S四边形EBHD=S四边形ABCD
    所以S四边形EFHG=S四边形EBHD=×S四边形ABCD=S四边形ABCD
    （1）如图④：四边形ABCD中,点E、F是AD的5等分点中最中间2个,点G、H是BC的5等分点中最中间2个,连接EG、FH,猜想：S四边形EFHG与S四边形ABCD之间有什么关系呢                       
    验证你的猜想：

    （2）问题解决：如图①,在四边形ABCD中,点E、F是AD的n等分点中最中间2个,点G、H是BC的n等分点中最中间2个,连接EG、FH,（其中n为奇数）
    那么S四边形EFHG与S四边形ABCD之间的关系为：                            （不必写出求解过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在边长为1的正方形网格中有两个三角形△ABC和△DEF，试证这两个三角形相似．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    在一个边长为a（单位：cm）的正方形ABCD中.

    （1）如图1，如果N是AD中点，F为AB中点，连接DF，CN.
    ①求证：DF=CN；
    ②连接AC.求DH:HE: EF的值；
    （2）如图2，如果点E、M分别是线段AC、CD上的动点，假设点E从点A出发，以cm/s速度沿AC向点C运动，同时点M从点C出发，以1cm/s的速度沿CD向点D运动，运动时间为t（t＞0），连结DE并延长交正方形的边于点F，过点M作MN⊥DF于H，交AD于N.判断命题“当点F是边AB中点时，则点M是边CD的三等分点”的真假，并说明理由. （4分）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在边长为4的正方形ABCD中，点P在AB上从A向B运动，连接DP交AC于点Q．

    （1）试证明：无论点P运动到AB上何处时，都有△ADQ≌△ABQ；
    （2）当点P在AB上运动到什么位置时，△ADQ的面积是正方形ABCD面积的；
    （3）若点P从点A运动到点B，再继续在BC上运动到点C，在整个运动过程中，当点P运动到什么位置时，△ADQ恰为等腰三角形．

    查看答案和解析>>

    同步练习册答案