
分析 (1)直接运用x2+(p+q)x+pq=(x+p)(x+q)分解因式得出即可;
(2)ax2+bx+c(a≠0)型的式子的因式分解的关键是把二次项系数a分解成两个因数a1,a2的积a1•a2,把常数项c分解成两个因数c1,c2的积c1•c2,并使a1c2+a2c1正好是一次项b,那么可以直接写成结果:ax2+bx+c=(a1x+c1)(a2x+c2);
(3)同(2);
(4)直接利用十字相乘法将y看作常数,分解因式得出答案即可;
(5)直接利用十字相乘法将m看作常数,分解因式得出答案即可;
(6)同(2),利用十字相乘法将m看作常数,分解因式得出答案即可.
解答 解:(1)x2+11x-26=(x+13)(x-2);
(2)2x2+x-6=(2x-3)(x+2);
(3)6x2-7x-3=(3x+1)(2x-3);
(4)x2-3xy+2y2=(x-2y)(x-y);
(5)x2-(2m+1)x+m(m+1)=(x-m)(x-m-1);
(6)mx2-(m+1)x+1=(mx-1)(x-1).
点评 此题主要考查了十字相乘法分解因式;熟练掌握十字相乘法分解因式,正确分解常数项是解题关键.


科目:初中数学 来源: 题型:选择题
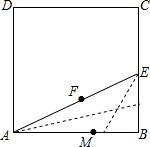 欧几里得在《几何原本》中,记载了用图解法解方程x2+ax=b2的方法,类似地可以用折纸的方法求方程x2+x-1=0的一个正根.如图,裁一张边长为1的正方形的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置B′,因而EB′=EB,类似地,在AB上折出点B″使AB″=AB′,表示方程x2+x-1=0的一个正根的线段是( )
欧几里得在《几何原本》中,记载了用图解法解方程x2+ax=b2的方法,类似地可以用折纸的方法求方程x2+x-1=0的一个正根.如图,裁一张边长为1的正方形的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置B′,因而EB′=EB,类似地,在AB上折出点B″使AB″=AB′,表示方程x2+x-1=0的一个正根的线段是( )| A. | 线段BB″ | B. | 线段AB″ | C. | 线段BE | D. | 线段AE |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
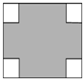 如图所示,在一个边长为12cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
如图所示,在一个边长为12cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com