Question

4．一般地，如果在一次实验中，结果落在区域D中每一个点都是等可能的，用A表示“实验结果落在D中的某个小区域M中”这个事件，那么事件A发生的概率P（A）=$\frac{M}{D}$（M和D分别表示相应区域的面积）．如图，现有一边长为a的等边△ABC，分别以此三角形的三个顶点为圆心，以一边的一半长为半径画圆与△ABC的内切圆有重叠（见图中阴影部分）；现在在等边△ABC内注射一个点，则该点落在△ABC内切圆中的概率是$\frac{\sqrt{3}π}{9}$．

Answer 1

分析 利用等边三角形以及其内切圆的性质以及锐角三角函数关系得出DO，AD的长，从而可以求得△ABC的面积和内切圆的面积，本题得以解决．

解答 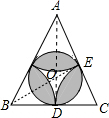解：作AD⊥BC于点D，作BE⊥AC于点E，
∵等边△ABC的边长为a，
∴∠OBD=30°，BD=$\frac{a}{2}$，AD=$\frac{\sqrt{3}a}{2}$
∴OD=BD•tan30°=$\frac{a}{2}•\frac{\sqrt{3}}{3}=\frac{\sqrt{3}a}{6}$，
∴内切圆⊙O的面积是：$π×（\frac{\sqrt{3}a}{6}）^{2}=\frac{π{a}^{2}}{12}$，
等边△ABC的面积是：$\frac{1}{2}×a×\frac{\sqrt{3}a}{2}=\frac{\sqrt{3}{a}^{2}}{4}$，
∴该点落在△ABC内切圆中的概率是：$\frac{\frac{π{a}^{2}}{12}}{\frac{\sqrt{3}{a}^{2}}{4}}=\frac{\sqrt{3}π}{9}$，
故答案为：$\frac{\sqrt{3}π}{9}$．

点评 此题主要考查了几何概率以及三角形内切圆的性质以及等边三角形的性质等知识，得出等边三角形与内切圆的关系是解题关键．