练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．二次函数y=3x2-6x-5顶点式为y=3（x-1）2-8，顶点为（1，-8），当-1＜x≤6时，最大值是-8，最小值是67．

    分析 先把二次项系数化为1，再加上一次项系数的一半的平方来凑完全平方式，把一般式转化为顶点式，即可得出顶点坐标；根据二次函数的性质结合自变量的取值范围即可求解．

    解答 解：y=3x2-6x-5=3（x2-2x）-5=3（x2-2x+1）-5-3=3（x-1）2-8，
    ∴顶点为（1，-8）；
    （2）∵抛物线y=3x2-6x-5开口向上，对称轴为x=1，
    ∴当-1＜x≤6时，x=1，y有最小值-8；x=6，y有最大值67；
    故答案为y=3（x-1）2-8，（1，-8），-8，67．

    点评 本题考查了二次函数解析式的三种形式，二次函数的性质及最值的求法，难度适中．把一般式转化为顶点式是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    2．方程x+$\sqrt{x}$=0的解是0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知方程组$\left\{\begin{array}{l}{x+y=3m}\\{x-y=m-1}\end{array}\right.$的解满足$\left\{\begin{array}{l}{x＜0}\\{y＞0}\end{array}\right.$，求m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知关于x的一元二次方程x2-2（m+1）x+m2-2m-3=0的两个不相等的实数根中，有一个根为0，是否存在实数k，使得x的方程x2-（k-m）x-k-m2+5m-2=0的两个根x1，x2之差的绝对值为1？若存在，求出k的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如图，在△ABC中，AB=AC，D、E在BC上，要证明△ABE≌△ACD还应补充的条件是∠AEB=∠ADC或∠BAE=∠CAD或BE=CD或BD=CE（只要求写出一种情况）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．数学课上，张老师出示图1和下面的条件：如图1，两块都含有30°角的直角三角板ABC和DEF有一条边在同一直线L上，∠ABC=∠DEF=90°，AB=1，DE=2．将直线EB绕点E逆时针旋转30°，交直线AD于点M．将图中的三角板ABC沿直线L向右平移．

    请你和小明同学一起尝试探究下列问题：
    （1）当点C与点F重合时，如图2所示，AM与DM是否相等？是；（填”是”或”否”）；
    （2）小明同学将图2中的三角板ABC绕点C逆时针旋转90°，将直线EB绕点E逆时针旋转30°，交直线AD于点M，如图3，过点B作EB的垂线交直线EM于G，连结AG，①求证：△ABG∽△CBE；②求AG的长．
    （3）小明同学又将图1中的三角板ABC绕点C逆时针旋转m度，0＜m≤90，原题中的其他条件保持不变，如图4，设CE=x，计算$\frac{AM}{DM}$的值（用含x的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

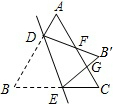    11．如图，等边三角形ABC中，点D，E分别在边AB，BC上，把△BDE沿直线DE翻折，使点B落在点B′处，DB′，EB′分别交边AC于点F，G，若∠ADF=95°，则∠EGC的度数为95°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．Rt△ABC中，∠ABC=90°，BD为角平分线交AC于点D，过点D作AC的垂线交Rt△ABC的直角边于点E．
    当∠A=45°，如图1时，点E和点B重合，易证：AB+BE=$\sqrt{2}$BD．
    当∠A＞45°，如图2时，AB、BE、BD是否存在上述数量关系？若存在，请证明：若不存在，请直接写出你的猜想，不必证明；
    当∠A＜45°时，如图3时，请直接判断AB、BE、BD是否存在上述数量关系？不需证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．用适当的方法解下列方程：
    （1）4（x-1）2=36；            
    （2）${x^2}-2\sqrt{5}x+1=0$；
    （3）（3x-1）（x+1）=4；        
    （4）（2x-3）2-3（2x-3）+2=0．

    查看答案和解析>>

    同步练习册答案