
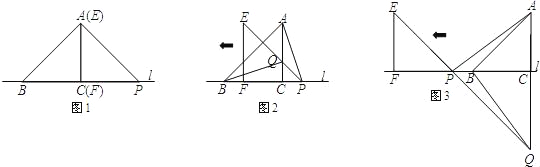
【题目】锐角为45°的直角三角形的两直角边长也相等,这样的三角形称为等腰直角三角形.我们常用的三角板中有一块就是这样的三角形,也可称它为等腰直角三角板.把两块全等的等腰直角三角板按如图1放置,其中边BC、FP均在直线l上,边EF与边AC重合.
(1)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想;
(2)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
【答案】见解析
【解析】试题分析:(1)延长BQ交AP于点M,根据等腰直角三角板的每一个锐角都是45°可得∠EPF=45°,然后求出∠CQP=45°,根据等角对等边的性质求出CQ=CP,然后利用边角边定理证明△BCQ与△ACP全等,再根据全等三角形对应边相等,即可证明BQ=AP,对应角相等可得∠CBQ=∠CAP,又∠CBQ+∠BQC=90°,所以∠CAP+∠AQM=90°,从而得到BQ⊥AP;
(2)延长QB交AP于点M,根据等腰直角三角板的每一个锐角都是45°可得∠EPF=45°,根据对顶角相等得到∠CPQ=45°,然后求出∠CQP=45°,根据等角对等边的性质求出CQ=CP,然后利用边角边定理证明△BCQ与△ACP全等,再根据全等三角形对应边相等,即可证明BQ=AP,对应角相等可得∠BQC=∠APC,又∠CBQ+∠BQC=90°,所以∠PBM+∠APC=90°,从而得到BQ⊥AP.
试题解析:(1)BQ=AP,BQ⊥AP.
证明:延长BQ交AP于点M,
∵△ABC和△EFP都是等腰直角三角板,
∴BC=AC,AC⊥BC,∠EPF=45°,
∴∠BCQ=∠ACP=90°,∠CQP=∠EPF=45°,
∴CQ=CP,
在△BCQ和△ACP中,
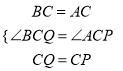 ,
,
∴△BCQ≌△ACP(SAS),
∴BQ=AP,∠CBQ=∠CAP,
∵∠BCQ=90°,
∴∠CBQ+∠BQC=90°,
∵∠BQC=∠AQM(对顶角相等),
∴∠CAP+∠AQM=90°,
∴∠AMB=90°,
∴BQ⊥AP;
(2)关系仍然成立:BQ=AP,BQ⊥AP.
证明:延长QB交AP于点M,
∵△ABC和△EFP都是等腰直角三角板,
∴BC=AC,AC⊥BC,∠EPF=45°,
∴∠BCQ=∠ACP=90°,
∵∠CQP=∠EPF=45°,
∴∠CPQ=∠CQP=45°,
∴CQ=CP,
在△BCQ和△ACP中,
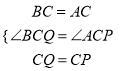 ,
,
∴△BCQ≌△ACP(SAS),
∴BQ=AP,∠BQC=∠APC,
∵∠BCQ=90°,
∴∠CBQ+∠BQC=90°,
∵∠PBM=∠QBC(对顶角相等),
∴∠PBM+∠APC=90°.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
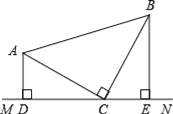
【题目】如图,在△ABC中∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)求证:△ADC≌△CEB;
(2)若AD=1,BE=2,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=x2﹣2x+3向上平移1个单位,平移后所得的抛物线的表达式为( )
A.y=x2﹣2x+4B.y=x2﹣2x+2C.y=x2﹣3x+3D.y=x2﹣x+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.对角线互相垂直的四边形是菱形B.对角线相等的菱形是正方形
C.对角线互相垂直且相等的四边形是正方形D.对角线相等的四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
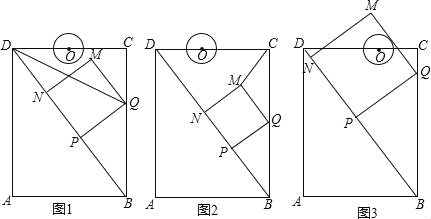
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3m/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t<).
(1)如图1,连接DQ平分∠BDC时,t的值为 ;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了节约用水,自建了一座污水净化站,今年一月份净化污水3万吨,三月份增加到3.63万吨,则这两个月净化的污水量每月平均增长的百分率为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,AB=BC=3,BD=BE=1,连结CD,AE.
求证:△BCD≌△BAE.
(2)在(1)的条件下,当![]() 时,延长CD交AE于点F,如图②,求AF的长.
时,延长CD交AE于点F,如图②,求AF的长.
(3)在(2)的条件下,线段BC上是否存在一点P,使得△PBD为等腰三角形?若存在,请直接写出满足△PBD为等腰三角形时,线段PB的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知实数a,b,c满足a>b,c是任意实数,则下列不等式中总是成立的是( )
A. a+c<b+c B. a-c>b-c C. ac<bc D. ac>bc
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com