
【题目】如图①,![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一点,
上一点,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 为
为![]() 中点,
中点,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,
,![]() ≌
≌![]() .
.
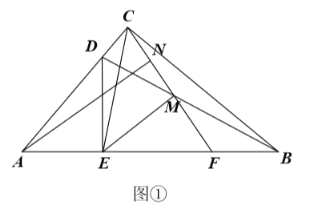
(1)求证:![]() ;
;
(2)求![]() 的大小;
的大小;
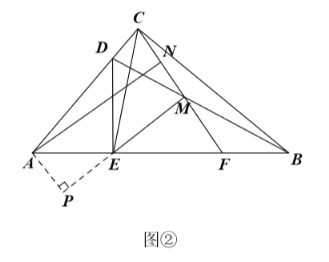
(3)如图②,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求证:四边形
,求证:四边形![]() 为矩形.
为矩形.
【答案】(1)证明见解析;(2)∠MEF=30°;(3)证明见解析.
【解析】
(1)利用直角三角形斜边中线的性质定理可得CM=![]() DB,EM=
DB,EM=![]() DB,问题得证;
DB,问题得证;
(2)利用全等三角形的性质,证明△DEM是等边三角形,即可解决问题;
(3)设FM=a,则AE=CM=EM=![]() a,EF=2a,推出
a,EF=2a,推出![]() ,
,![]() ,得到AN∥PM,易证四边形ANMP是平行四边形,结合∠P=90°即可解决问题.
,得到AN∥PM,易证四边形ANMP是平行四边形,结合∠P=90°即可解决问题.
解:(1)证明:如图①中,
∵DE⊥AB,
∴∠DEB=∠DCB=90°,
∵DM=MB,
∴CM=![]() DB,EM=
DB,EM=![]() DB,
DB,
∴CM=EM;
(2)解:∵△DAE≌△CEM,CM=EM,
∴AE=ED=EM=CM=DM,∠AED=∠CME=90°
∴△ADE是等腰直角三角形,△DEM是等边三角形,
∵∠AED=∠DEF=90°,∠DEM=60°,
∴∠MEF=30°;
(3)证明:如图②中,设FM=a.
由(2)可知△ADE是等腰直角三角形,△DEM是等边三角形,∠MEF=30°,
∴AE=CM=EM=![]() a,EF=2a,
a,EF=2a,
∵CN=NM,
∴MN=![]() a,
a,
∴![]() ,
,![]() ,
,
∴EM∥AN,
∵AP⊥PM,MN⊥PM,
∴AP∥MN,
∴四边形ANMP是平行四边形,
∵∠P=90°,
∴四边形ANMP是矩形.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() 各顶点的坐标分别为
各顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.
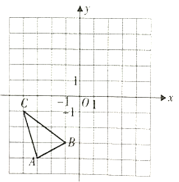
(1)画出![]() 以点B为旋转中心,按顺时针方向旋转
以点B为旋转中心,按顺时针方向旋转![]() 后得到的
后得到的![]() ;
;
(2)将![]() 先向右平移5个单位长度,再向上平移3个单位长度,得到
先向右平移5个单位长度,再向上平移3个单位长度,得到![]() .
.
①在图中画出![]() ,并写出点A的对应点
,并写出点A的对应点![]() 的坐标;
的坐标;
②如果将![]() 看成是由
看成是由![]() 经过一次平移得到的,请指出这一平移的平移方向和平移距离.
经过一次平移得到的,请指出这一平移的平移方向和平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级某班级为了促进同学养成良好的学习习惯,每天都对同学进行学规管理记分.如下是小李同学第8周学规得分(规定:加分为“+”,扣分为“﹣”).

(1)第8周小李学规得分总计是多少?
(2)根据班规,一学期里班级还会将同学每周的学规得分进行累加.已知小李同学第7周末学规累加分数为98分,若他在第9周末学规累加分数达到105分,则他第9周的学规得分总计是多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() ,将
,将![]() 绕点
绕点![]() 顺时针得到
顺时针得到![]() (点
(点![]() ,
,![]() 的对应点分别为
的对应点分别为![]() ,
,![]() ),射线
),射线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() .
.
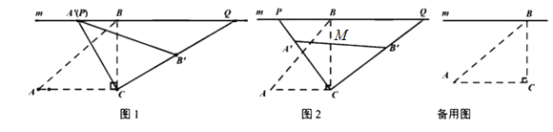 (1)如图1,当
(1)如图1,当![]() 与
与![]() 重合时,求
重合时,求![]() 的度数;
的度数;
(2)如图2,设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 为
为![]() 的中点时,求线段
的中点时,求线段![]() 的长;
的长;
(3)在旋转过程时,当点![]() 分别在
分别在![]() ,
,![]() 的延长线上时,试探究四边形
的延长线上时,试探究四边形![]() 的面积是否存在最小值.若存在,求出四边形
的面积是否存在最小值.若存在,求出四边形![]() 的最小面积;若不存在,请说明理由.
的最小面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,点P是对角线AC上一点,连结BP,过P作PQ⊥BP,PQ交CD于Q,若AP=![]() ,CQ=3,则四边形PBCQ的面积为_______.
,CQ=3,则四边形PBCQ的面积为_______.
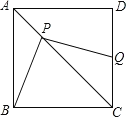
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() .在下列解答中,填空(理由或数学式):
.在下列解答中,填空(理由或数学式):
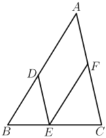
解:∵![]() (已知),
(已知),
∴![]() (______),
(______),
∵![]() (已知),
(已知),
∴∠______=∠______(等量代换),
∴![]() ______(______),
______(______),
∴![]() (______).
(______).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,线段AB、CD相交于点O,连结AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于点M、N.试解答下列问题:

(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系;
(2)仔细观察,在图2中“8字形”有多少个;
(3)图2中,当∠D=50°,∠B=40°时,求∠P的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:如图,射线![]() 在
在![]() 上方,射线
上方,射线![]() 在
在![]() 下方,
下方,![]() ,
,![]() (
(![]() ,
,![]() ),
),![]() 与
与![]() 分别是
分别是![]() 和
和![]() 的平分线.
的平分线.
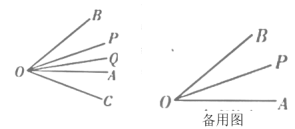
操作发现:(1)当![]() ,
,![]() 时,求
时,求![]() 的度数;
的度数;
(2)继续探究,当![]() 固定不变,把
固定不变,把![]() 扩大为
扩大为![]() 时,求
时,求![]() 的度数;
的度数;
探索发现:(3)在完成(1)(2)时,小亮发现![]() 与
与![]() 之间存在一个固定的数量关系.你认为小亮说的对吗?请说明理由.
之间存在一个固定的数量关系.你认为小亮说的对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A. 20 B. 25 C. 30 D. 32
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com