
 解:(1)∵抛物线顶点坐标(2,-1),
解:(1)∵抛物线顶点坐标(2,-1), ,
, 或
或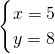 ,
,

科目:初中数学 来源: 题型:
| 2 |
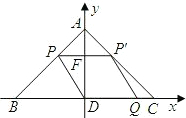 向作匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为y,DQ=x.
向作匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为y,DQ=x.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,⊙C经过原点且与两坐标分别交于点A与点B,点A的坐标为(0,6),点M是圆上弧BO的中点,且∠BMO=120°.
如图,⊙C经过原点且与两坐标分别交于点A与点B,点A的坐标为(0,6),点M是圆上弧BO的中点,且∠BMO=120°.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知Rt△AOB在平面直角坐标系中,∠AOB=90°,∠BAO=30°,且A的坐标为(3,0),⊙C的圆心坐标为(-1,0),半径为1,若D是⊙C上的一个动点,线段DA与y轴交与点E.求:
如图,已知Rt△AOB在平面直角坐标系中,∠AOB=90°,∠BAO=30°,且A的坐标为(3,0),⊙C的圆心坐标为(-1,0),半径为1,若D是⊙C上的一个动点,线段DA与y轴交与点E.求:查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 16 |
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源:第26章《二次函数》中考题集(41):26.3 实际问题与二次函数(解析版) 题型:解答题
 ,D为斜边BC的中点.点P由点A出发沿线段AB作匀速运动,P′是P关于AD的对称点;点Q由点D出发沿射线DC方向作匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为y,DQ=x.
,D为斜边BC的中点.点P由点A出发沿线段AB作匀速运动,P′是P关于AD的对称点;点Q由点D出发沿射线DC方向作匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为y,DQ=x.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com