
【题目】已知平行四边形ABCD.
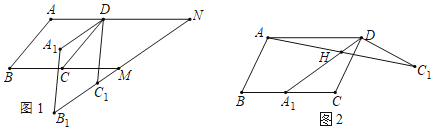
(1)如图1,将ABCD绕点D逆时针旋转一定角度得到A1B1C1D,延长B1C1,分别与BC、AD的延长线交于点M、N.
①求证:∠BMB1=∠ADA1;
②求证:B1N=AN+C1M;
(2)如图2,将线段AD绕点D逆时针旋转,使点A的对应点A1落在BC上,将线段CD绕点D逆时针旋转到C1D的位置,AC1与A1D交于点H.若H为AC1的中点,∠ADC1+∠A1DC=180°,A1B=nA1C,试用含n的式子表示![]() 的值.
的值.
【答案】(1)①见解析;②见解析;(2)2n+1
【解析】
(1)①先判断出∠BMB1=∠N,再判断出∠N=∠ADA1,即可得出结论;
②先判断出∠DCE=∠B=∠B1=∠DC1F,DC=DC1,得出△DCE≌△DC1F,得出DE=DF,进而判断出Rt△DEM≌Rt△DMF,得出∠DME=∠DMF,进而判断出DN=MN,即可得出结论;
(2)先判断出AT=2DH,得出∠ADT=∠A1DC,进而判得出△A1DC≌△ADT,得出A1C=AT=2DH.即可得出结论.
解:(1)①∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠BMB1=∠N,
由旋转知,四边形A1B1C1D是平行四边形,
∴A1D∥B1C1,
∴∠N=∠ADA1,
∴∠BMB1=∠ADA1;
②如图,连接DM,过D作DE⊥BC于E,作DF⊥MN于F,
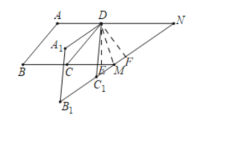
∴∠DEC=∠DFC1=90°,
显然,∠DCE=∠B=∠B1=∠DC1F,DC=DC1,
∴△DCE≌△DC1F(AAS),
∴DE=DF,
∵DM=DM,
∴Rt△DEM≌Rt△DMF(HL),
∴∠DME=∠DMF,
又∵AN∥BM,
∴∠DME=∠MDN,
∴∠DMN=∠MDN,
∴DN=MN,
又AD=BC=B1C1,
∴B1N=B1C1+C1M+MN=AD+C1M+DN=AN+C1M;
(2)如图,延长C1D至点T,使DT=DC1,连接AT,
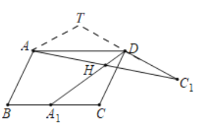
∵H为AC1的中点,
∴AT=2DH(三角形中位线定理).
∵∠ADC1+∠A1DC=180°,∠ADC1+∠ADT=180°,
∴∠ADT=∠A1DC,
由旋转知,A1D=AD,DC=DC1=DT,
∴△A1DC≌△ADT(SAS),
∴A1C=AT=2DH.
设DH=a,则A1C=AT=2a,
A1B=nA1C=2an,A1D=AD=BC=A1B+A1C=2an+2a,
∴A1H=A1D﹣DH=2an+2a﹣a=2an+a,
∴![]() =2n+1.
=2n+1.


科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是_________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中,我们经历了“确定函数的解析式利用函数图象研究其性质﹣运用函数解决问题”的学习过程.在画函数图象时,我们可以通过描点或平移或翻折等方法画出函数图象、下面我们対函数y=|![]() ﹣1|展开探索,请补充以下探索过程:
﹣1|展开探索,请补充以下探索过程:
(1)列表
x | … | ﹣1 | ﹣ | ﹣ | ﹣ | 0 |
|
|
| … |
|
|
| 2 |
|
|
| 3 | … | |
y | … |
|
|
|
| 2 |
| 3 | a | … | 3 | 1 |
| 0 |
|
| b |
| … | |
直接写出函数自变量x的取值范围,及a= ,b= ;
(2)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象,并写出这个函数的一条性质: .
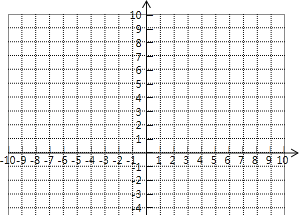
(3)若方程|![]() ﹣1|=m有且只有一个解,直接写出m的值: .
﹣1|=m有且只有一个解,直接写出m的值: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则∠BED的度数为( )
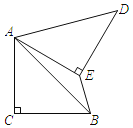
A.100°B.120°C.135°D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“光”、“明”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“光明”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直线![]() 上有相距
上有相距![]() 的两点
的两点![]() 和
和![]() (点
(点![]() 在点
在点![]() 的右侧),以
的右侧),以![]() 为圆心作半径为
为圆心作半径为![]() 的圆,过点
的圆,过点![]() 作直线
作直线![]() .将
.将![]() 以
以![]() 的速度向右移动(点
的速度向右移动(点![]() 始终在直线
始终在直线![]() 上),则
上),则![]() 与直线
与直线![]() 在______秒时相切.
在______秒时相切.

A.3B.3.5C.3或4D.3或3.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图:
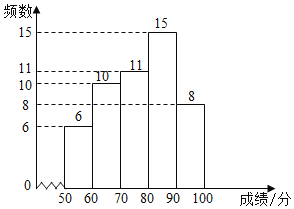
b.七年级成绩在![]() 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com