
����Ŀ��ij�������������Բ��ɻ��������Ĵ�������Ϊ90Ԫ/�֣��ɻ��������ķּ�������ҲΪ90Ԫ/�֣��ּ���ٱ������ҵ���գ����ռ۸����±���
�������� | ֽ�� | ������ | ������ | ������ |
���յ��ۣ�Ԫ/�֣� | 500 | 800 | 500 | 200 |
���˽⣬�ɻ�������ռ����������60%������![]() ����С��12�·ݲ��������������ֱ�Ϊ100��,100�ֺ�
����С��12�·ݲ��������������ֱ�Ϊ100��,100�ֺ�![]() ��.
��.
(1)��֪![]() С�������������������������5����ֽ�������������������2��.�������������Ϊ
С�������������������������5����ֽ�������������������2��.�������������Ϊ![]() �֣���
�֣���![]() С���ɻ���������______�֣����в�����������_____��(�ú�
С���ɻ���������______�֣����в�����������_____��(�ú�![]() �Ĵ���ʽ��ʾ)
�Ĵ���ʽ��ʾ)
(2)![]() С��ֽ�����������������Ϊ35�֣����¿ɻ������������ܽ��۳��������������Ѻ�����16500Ԫ.��12�·ݸ�С���ɻ�������������������������.
С��ֽ�����������������Ϊ35�֣����¿ɻ������������ܽ��۳��������������Ѻ�����16500Ԫ.��12�·ݸ�С���ɻ�������������������������.
(3)![]() С�������������벣���������Ļ����ܶ�ǡ�����,���пɻ��������Ļ����ܽ��Ϊ12000Ԫ.���С����������������Ϊ
С�������������벣���������Ļ����ܶ�ǡ�����,���пɻ��������Ļ����ܽ��Ϊ12000Ԫ.���С����������������Ϊ![]() �֣���
�֣���![]() ��
��![]() ��������ϵ.
��������ϵ.
���𰸡�(1)60��![]() ��(2)
��(2)![]() С��12�·ݿɻ�����������������������5�֣�(3)
С��12�·ݿɻ�����������������������5�֣�(3)![]() .
.
��������
��1����AС���������������Կɻ���������ռ�ٷֱȼ�������ɻ�����������������x��ʾ��������������ֽ�������������������������������������
��2����12�·�![]() С����������������Ϊ
С����������������Ϊ![]() �֣�����x��ʾ�����������������������ݵ��¿ɻ������������ܽ��۳��������������Ѻ�����16500Ԫ�з������x��ֵ���ɣ�
�֣�����x��ʾ�����������������������ݵ��¿ɻ������������ܽ��۳��������������Ѻ�����16500Ԫ�з������x��ֵ���ɣ�
��3�������������벣���������Ļ����ܶ�ǡ����ȿ���a��ʾ���������������������������ֽ����������������������������пɻ��������Ļ����ܽ��Ϊ12000Ԫ���ɵó�a��m��������ϵ.
��1���߿ɻ�������ռ����������60%��AС����������������100�֣�
��ɻ�������ռ��������Ϊ��100��60%=60���֣���
�߽����������������������5����ֽ�������������������2��.�����������Ϊ![]() �֣�
�֣�
�����������������5x��ֽ������������2x��
�ಣ���������У�60-5x-2x-x=(60-8x)�֣�
�ʴ�Ϊ��60��![]()
��2����12�·�![]() С����������������Ϊ
С����������������Ϊ![]() �֣�
�֣�
�ಣ������������Ϊ![]() �֣���
�֣���![]() �֣�
�֣�
��![]()
��ã�![]()
��![]() С��12�·ݿɻ�����������������������5��.
С��12�·ݿɻ�����������������������5��.
��3���貣������������Ϊy�֣�
����������������Ϊ![]() �֣��������벣���������Ļ����ܶ���ȣ�
�֣��������벣���������Ļ����ܶ���ȣ�
��200y=800a��
��ã�y=4a��
�ಣ������������Ϊ![]() �֣�
�֣�
��ֽ�������������������Ϊ![]() �֣�
�֣�
�����пɻ��������Ļ����ܽ��Ϊ12000Ԫ��
��![]() ��
��
����ã�![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����һ��չ���������е����900��ѧУȥ��ѧ������ѧУ��������ѧ�α����ڼ����ˣ���������������ԭ·���лؼң��õ���ѧ�α�����������ԭ·�������г�����ѧУ����֪С�������г����ٶ����������ٶȵ�3�������д�ѧУ�������õ�ʱ����������г��Ӽҵ�ѧУ���õ�ʱ���10����. С�������г����ٶ��Ƕ�����ÿ�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
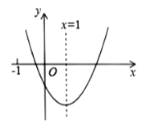
����Ŀ�����κ���![]() ��
��![]() ����ͼ����ͼ��ʾ���Գ���Ϊ
����ͼ����ͼ��ʾ���Գ���Ϊ![]() ���������н��ۣ���
���������н��ۣ���![]() �� �ڵ�
�� �ڵ�![]() ʱ��
ʱ��![]() ����
����![]() ����
����![]() ��������ȷ�Ľ�����__________��
��������ȷ�Ľ�����__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�ı߳�Ϊ6cm����E��M�ֱ����߶�BD��AD�ϵĶ��㣬����AE���ӳ�������BC��F����M��MN��AF������ΪH������AB�ڵ�N.
(1)��ͼ�٣�����M���D�غϣ���֤��AF��MN��
(2)��ͼ�ڣ�����M�ӵ�D��������1cm/s���ٶ���DA���A�˶���ͬʱ��E�ӵ�B��������![]() cm/s���ٶ���BD���D�˶����˶�ʱ��Ϊts.
cm/s���ٶ���BD���D�˶����˶�ʱ��Ϊts.
����BF��ycm����y����t�ĺ�������ʽ��
�ڵ�BN��2ANʱ������FN����FN�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦ���������ɸ�ij�ֱʼDZ�����ѧ�����ס��������̵궼���㹻���������ֱʼDZ������۶���ÿ��6Ԫ�����̵�Ĵ��������ǣ��������ֱʼDZ�����������5��ʱ��ԭ�����ۣ�����5��ʱ���������ְ�ԭ�۵�7������.���̵�����۷����ǣ�һ�ɰ���۵�8������.
��1��������ʦҪ����![]() �����ֱʼDZ������ú�
�����ֱʼDZ������ú�![]() ��ʽ�ӷֱ��ʾ����ʦ�����̵�����̵깺��ȫ�����ֱʼDZ�����ķ���.
��ʽ�ӷֱ��ʾ����ʦ�����̵�����̵깺��ȫ�����ֱʼDZ�����ķ���.
��2������ʦ������ٸ����ֱʼDZ�ʱ�����ס��������̵깺�����������ͬ��
��3��������ʦ��Ҫ20�����ֱʼDZ����ס����ļ��̵깺����Żݣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��д�������
��1����1+2��_____��
��2����1��1��_____��
��3������3��3��_____��
��4��6������1![]() ����_____��
����_____��
��5������1��2n������1��2n��1��_____��n����������
��6������4x��0�Ľ�Ϊ_____��
��7�����̩�![]() x��2�Ľ�Ϊ_____��
x��2�Ľ�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
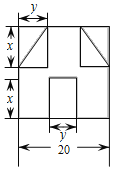
����Ŀ����������jiong�������Ƿ���������������һ���������Ƶ����飮��ͼ��ʾ��һ�ű߳�Ϊ20�������ε�ֽƬ����ȥ����һ����Сֱ�������κ�һ�������εõ�һ����������ͼ������Ӱ���֣������ȥ��С�����α߳�Ϊx��y����ȥ������Сֱ�������ε���ֱ�DZ߳�Ҳ�ֱ�Ϊx��y��
��1���ú���x��y�Ĵ���ʽ��ʾͼ������������Ӱ���֣��������
��2����x��y��Ϊ����ʱ�����ʱ�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Ϊʲô�κ�����ѭ��С��������д�ɷ�����ʽ������Ľ����̻������ԭ��ͷ�����
�Ķ����в��ϣ�
���⣺����һԪһ�η��̽�0.![]() ���ɷ�����
���ɷ�����
�⣺��0.![]() ��x��
��x��
�������߶�����10���ɵ�10��0.![]() ��10x
��10x
��0.![]() ��0.777������֪10��0.
��0.777������֪10��0. ![]() ��7.777����7+0.
��7.777����7+0.![]()
��7+x��10x����������Ὣ�������߶�����10�����ã�
�ɽ��x��![]() ����0.
����0.![]() ��
��![]() ��
��
��1����գ���0.![]() д�ɷ�����ʽΪ�� ����
д�ɷ�����ʽΪ�� ����
��2���������������������������С�����ɷ�����Ҫ��д������һԪһ�η��̽��н��Ĺ��̣���0.![]() ����0.43
����0.43![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com