
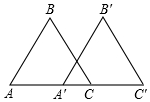
 如图,△A′B′C′是由△ABC沿射线AC方向平移20cm得到,若AC=30cm,则A′C=10cm.
如图,△A′B′C′是由△ABC沿射线AC方向平移20cm得到,若AC=30cm,则A′C=10cm. 科目:初中数学 来源: 题型:选择题
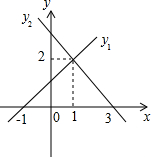 已知函数y1=k1x+b1与函数y2=k2x+b2的图象如图所示,则不等式y1>y2的解集是( )
已知函数y1=k1x+b1与函数y2=k2x+b2的图象如图所示,则不等式y1>y2的解集是( )| A. | x<1 | B. | x>1 | C. | x<2 | D. | x>3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
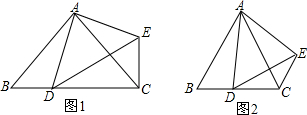 在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
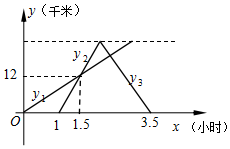 甲乙两人先后由A地沿同一路线前往B地,甲先出发,一小时后乙再出发,半小时后在离A地12千米处乙追上甲,此时两人正好到达AB的中点.然后两人各自保持原速不变,先后到达B地.若甲由A地出发的行驶时间为x小时,甲、乙离开A地的距离为y1千米和y2千米,函数图象如图所示.
甲乙两人先后由A地沿同一路线前往B地,甲先出发,一小时后乙再出发,半小时后在离A地12千米处乙追上甲,此时两人正好到达AB的中点.然后两人各自保持原速不变,先后到达B地.若甲由A地出发的行驶时间为x小时,甲、乙离开A地的距离为y1千米和y2千米,函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
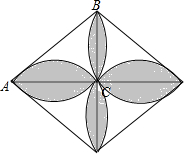 已知,在直角三角形ABC中,∠ACB=90°,AC=8,BC=6,AB=10,以AB边为直径作半圆,把4个相同的直角三角形通过一定的图形运动拼成四叶草的形状(如图所示),求阴影部分的面积.
已知,在直角三角形ABC中,∠ACB=90°,AC=8,BC=6,AB=10,以AB边为直径作半圆,把4个相同的直角三角形通过一定的图形运动拼成四叶草的形状(如图所示),求阴影部分的面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
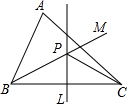 如图,锐角三角形ABC中,直线PL为BC的垂直平分线,射线BM平分∠ABC,PL与BM相交于点P.若∠A=57°,∠ACP=27°,则∠BCP=32度.
如图,锐角三角形ABC中,直线PL为BC的垂直平分线,射线BM平分∠ABC,PL与BM相交于点P.若∠A=57°,∠ACP=27°,则∠BCP=32度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com