
分析 根据二次函数定义可得$\left\{\begin{array}{l}{{m}^{2}-2m-1=2}\\{{m}^{2}-m≠0}\end{array}\right.$,解之可得m的值,从而可得函数解析式及各项系数、常数项.
解答 解:根据题意可得$\left\{\begin{array}{l}{{m}^{2}-2m-1=2}\\{{m}^{2}-m≠0}\end{array}\right.$,
解得:m=-1或m=3,
当m=-1时,二次函数为y=2x2-4x+1,其二次项系数为2,一次项系数为-4,常数项为1;
当m=3时,二次函数为y=6x2+9,其二次项系数为6,一次项系数为0,常数项为9.
点评 本题主要考查二次函数的定义,根据二次函数的定义得出关于m的方程,解之得出m的值是解题的关键.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:选择题
| A. | (-5,4) | B. | (4,3) | C. | (-1,-2) | D. | (-2,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
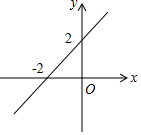 一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是x>-2;不等式kx+b<2的解集是x<0;当x<0时,y的取值范围是y<2;当x>-2时,y的取值范围是y>0.
一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是x>-2;不等式kx+b<2的解集是x<0;当x<0时,y的取值范围是y<2;当x>-2时,y的取值范围是y>0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
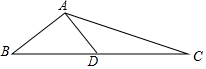 如图,在△ABC中,AB=5,AC=13,边BC上的中线AD=6.
如图,在△ABC中,AB=5,AC=13,边BC上的中线AD=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 《九章算术》中记载:“今有竹高一丈,未折抵地,去根三尺,问折者高几何?”译文:有一根竹子原高一丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?我们用线段OA和线段AB来表示竹子,其中线段AB表示竹子折断部分,用线段OB表示竹梢触地处离竹根的距离,则竹子折断处离地面的高度OA是4.55尺.
《九章算术》中记载:“今有竹高一丈,未折抵地,去根三尺,问折者高几何?”译文:有一根竹子原高一丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?我们用线段OA和线段AB来表示竹子,其中线段AB表示竹子折断部分,用线段OB表示竹梢触地处离竹根的距离,则竹子折断处离地面的高度OA是4.55尺.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com